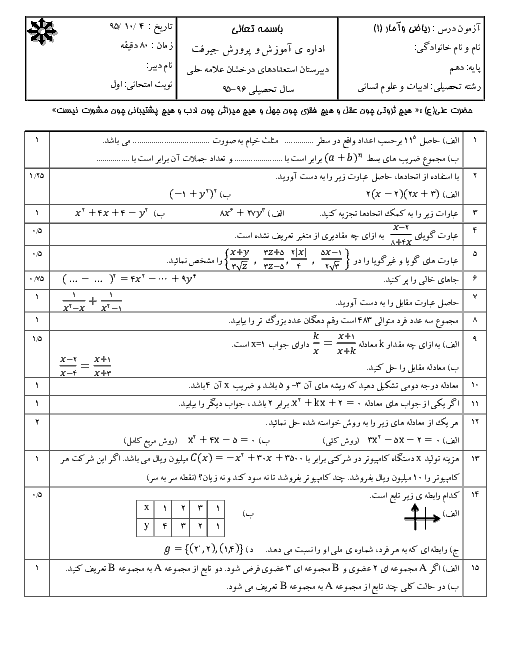
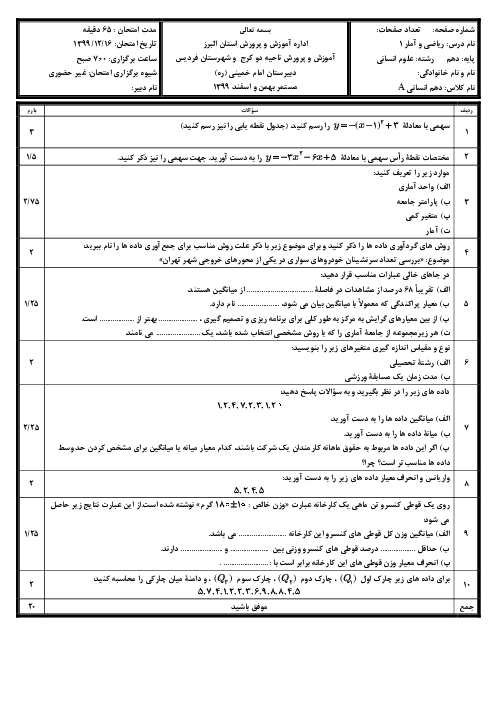
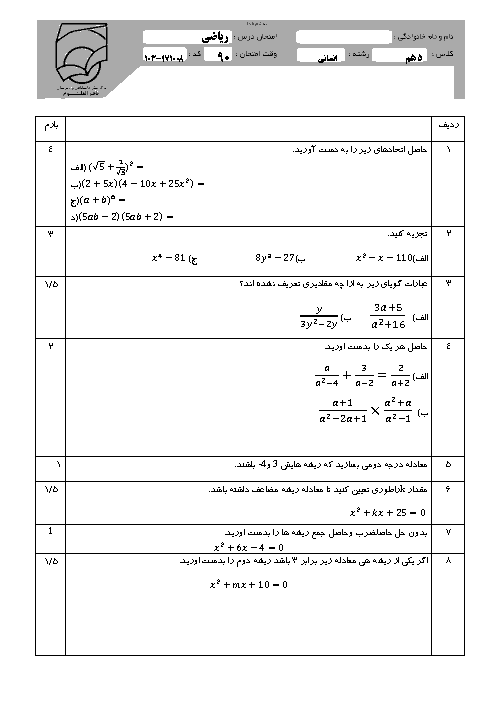
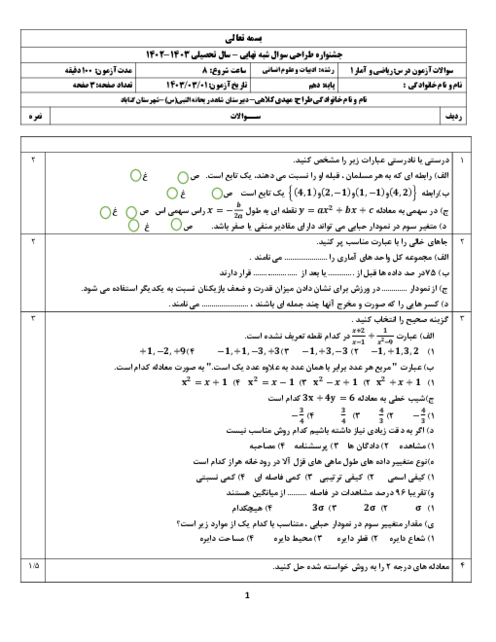
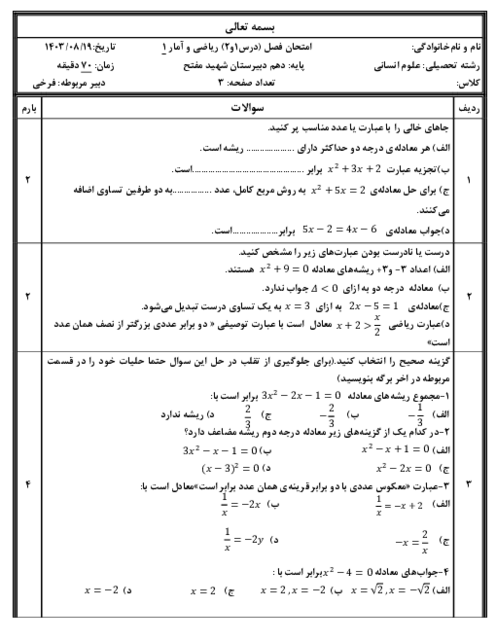
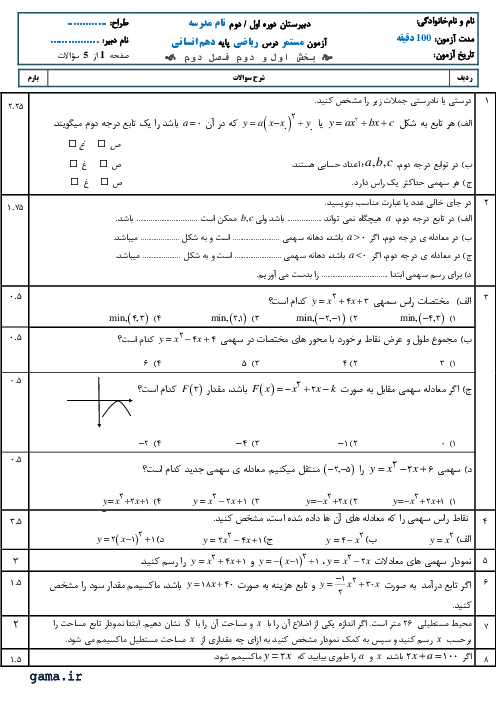
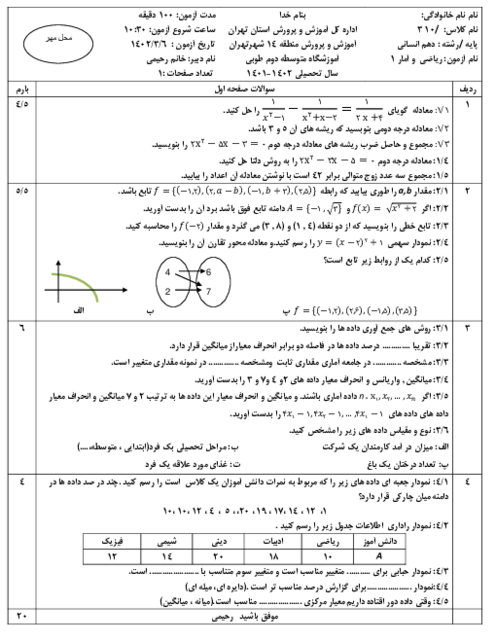
درس 2: معیارهای گرایش به مرکز
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
میانگین 100 دادهٔ آماری برابر 2/5 است. اگر تعدادی دادهٔ دیگر با میانگین 4 به آنها اضافه کنیم، میانگین کل دادهها برابر 3/75 میشود، تعداد دادههای اضافه شده کدام است؟