درس 2: توابع پلکانی و قدر مطلقی
ریاضی و آمار (2)
یازدهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
كدام گزينه میتواند ضابطۀ نمودار تابع مقابل باشد؟
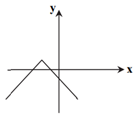
1 )
$y=\left| x+2 \right|-1$
2 )
$y=\left| x-2 \right|-1$
3 )
$y=-\left| x-2 \right|+1$
$y=-\left| x+2 \right|+1$