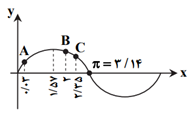
نكته: اگر $D$ اندازهٔ زاويه‌ای برحسب درجه و $R$ اندازهٔ آن برحسب راديان باشد، آن‌گاه: $\frac{D}{180}=\frac{R}{\pi }$

ابتدا با استفاده از نكتۀ بالا اندازهٔ ${{2}^{{}^\circ }}$ را برحسب راديان به‌دست می‌آوريم: 

$\frac{2}{180}=\frac{R}{\pi }\Rightarrow R=\frac{2}{180}\times \pi \Rightarrow R=\frac{\pi }{90}$

اکنون با فرض $\pi =3/14$ داریم:

$\frac{\pi }{90}=0/03,\frac{3\pi }{4}=2/35$

بنابراین: $\operatorname{Sin}{{2}^{{}^\circ }}=\operatorname{Sin}{{\frac{\pi }{90}}^{rad}}=\operatorname{Sin}0/{{03}^{rad}}$، $\operatorname{Sin}{{2}^{rad}}$ و $\operatorname{Sin}{{\frac{3\pi }{4}}^{rad}}=\operatorname{Sin}2/{{35}^{rad}}$ به‌ترتیب عرض نقاط $A$، $B$ و $C$ روی نمودار هستند، بنابراين گزينۀ 2 پاسخ است.