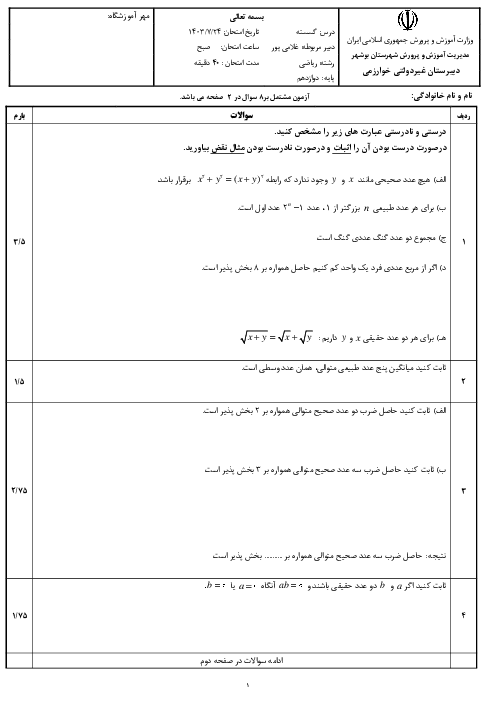
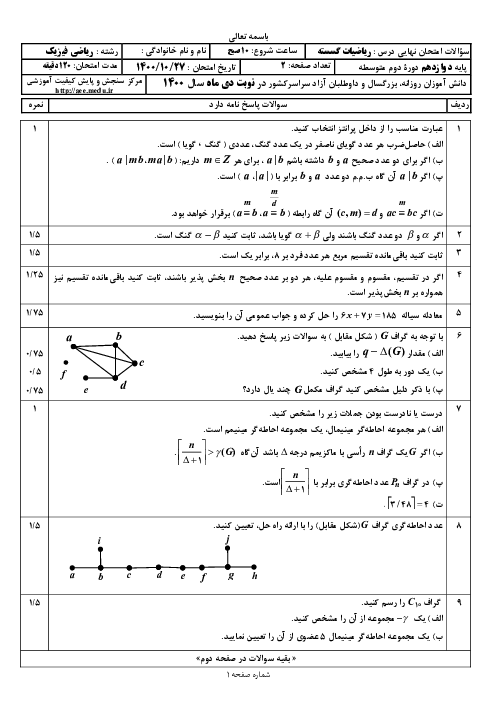
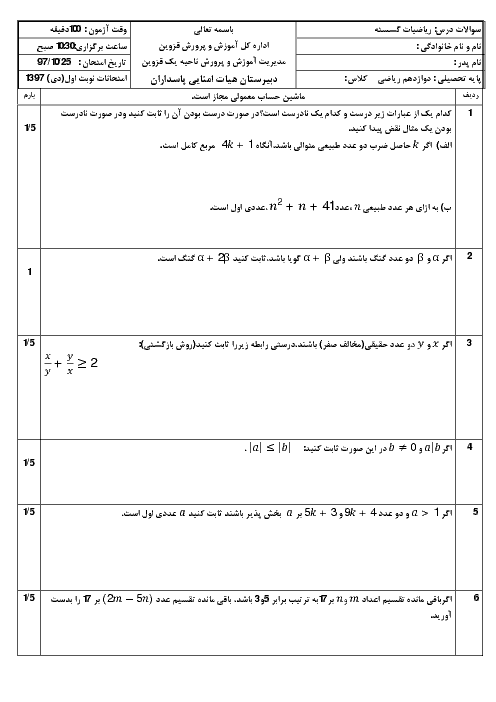
فرض کنید $A=\overline{a35b2}$، اگر $A$ بر 36 بخش‌پذیر باشد، آ‌ن‌گاه $A\overset{4}{\mathop{=}}\,0$ و $A\overset{9}{\mathop{=}}\,0$. از طرف دیگر می‌دانیم 

$\left\{ \begin{align}  & A\overset{4}{\mathop{=}}\,b2\overset{4}{\mathop{=}}\,10b+2\overset{4}{\mathop{=}}\,2b+2 \\  & A\overset{9}{\mathop{=}}\,a+3+5+b+2\overset{9}{\mathop{=}}\,a+b+10\overset{9}{\mathop{=}}\,a+b+1 \\ \end{align} \right.$

اکنون از اینکه $A\overset{4}{\mathop{=}}\,0$ و $A\overset{9}{\mathop{=}}\,0$ نتیجه می‌گیریم

$\left\{ \begin{align}  & 2b+2\overset{4}{\mathop{=}}\,0\Rightarrow 2b\overset{4}{\mathop{=}}\,-2\Rightarrow b\overset{\frac{4}{(4,2)}}{\mathop{=}}\,-1\Rightarrow b\overset{2}{\mathop{=}}\,-1 \\  & a+b+1\overset{9}{\mathop{=}}\,0\Rightarrow a+b\overset{9}{\mathop{=}}\,-1 \\  & \xrightarrow{0\le a+b\le 18}a+b=8ya\,a+b+17 \\ \end{align} \right.$

از اینکه $b\overset{2}{\mathop{=}}\,-1$ نتیجه می‌گیریم $b$ برابر 1، 3، 5، 7، یا 9 است.

با جای گذاری در دو معادلهٔ دیگر نتیجه می‌گیریم جواب‌های قابل قبول برای $(a,b)$ عبارت‌اند از :

$(7,1),(5,3),(3,5),(1,7),(8,9)$