نکته: اگر $x=a$ و $x=\beta $ صفرهای یک سهمی باشند، آنگاه معادلهٔ سهمی به صورت $f(x)=a(x-a)(x-\beta )$ است.

نکته: اگر $x=a$ و $x=\beta $ صفرهای یک سهمی باشند، آنگاه طول رأس این سهمی $x=\frac{a+\beta }{2}$ است.

راه حل اول:

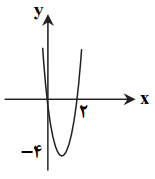
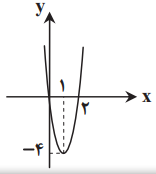
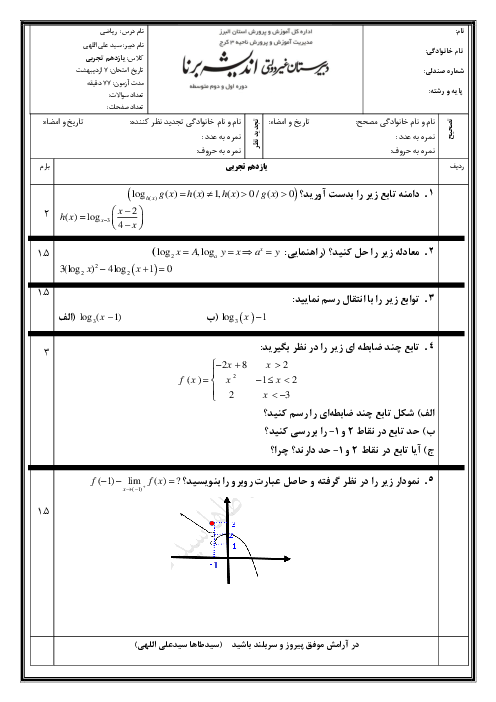
با توجه به نمودار، ریشه‌های معادلهٔ $f(x)=0$ عبارتند از $x=0$ و $x=2$، پس از نکات بالا نتیجه می‌گیریم طول رأس این سهمی برابر $x=\frac{0+2}{2}=1$ و ضابطهٔ سهمی به‌صورت $f(x)=ax(x-2)$ است.

اکنون با توجه به اینکه عرض رأس سهمی برابر 4- است، خواهیم داشت:

$f(1)=-4\Rightarrow a(-1)=-4\Rightarrow a=4$

پس $f(x)=4x(x-2)$، در نتیجه:

$f(3)=12$

راه حل دوم: نکته: طول رأس سهمی $f(x)=a{{x}^{2}}+bx+c$ به صورت $x=-\frac{b}{2a}$ است.

با توجه به نمودار $f(0)=f(2)=0$، پس:

$\left\{ \begin{matrix}f(0)=c=0  \\ f(2)=4a+2b+c=0\xrightarrow{c=0}4a+2b=0\Rightarrow b=-2a\Rightarrow -\frac{b}{2a}=1  \\\end{matrix} \right.$     

 بنابراین طول رأس سهمی برابر $X=1$ است. با توجه به نمودار، عرض رأس سهمی برابر 4- است، پس:

$f(1)=-4\Rightarrow a+b+c=-4\xrightarrow{c=0}a+b=-4\xrightarrow{b=-2a}a-2a=-4\Rightarrow a=4\xrightarrow{b=-2a}b=-8$

پس $f(x)=4{{x}^{2}}-8x$. در نتیجه: $f(3)=36-24=12$

صفحهٔ 18 ریاضی 2