قسمت 5: توان در مدارهای الکتریکی
فیزیک (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
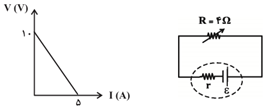
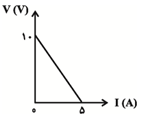
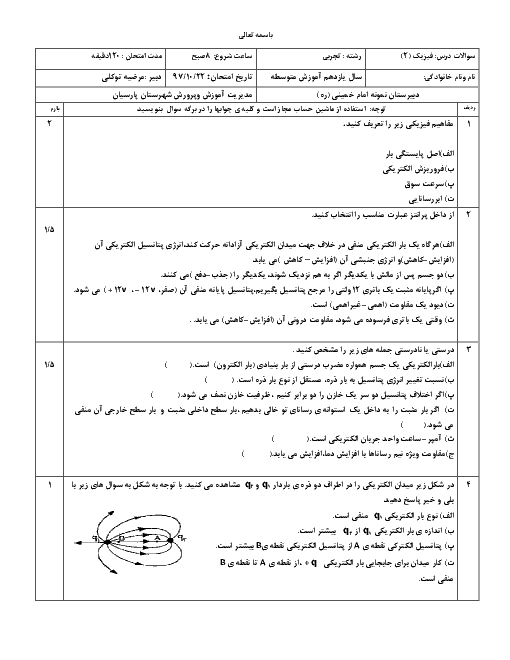
شكل زير، نمودار اختلاف پتانسيل دو سر مولد را برحسب جريان عبوری از آن نشان میدهد. اگر مقاومت متغير $R$ نصف شود، توان خروجی مولد چند برابر میشود؟