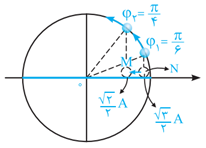
گام اول: نوسانگر 2 ثانیه پس از شروع حرکت، در مکان ${{x}_{N}}=\frac{\sqrt{3}}{2}A$ قرار داشته و به سمت مرکز حرکت می‌کند. بنابراین با توجه به مشتقات $\frac{\pi }{6}$، فاز نوسانگر در لحظهٔ $t=2s$ برابر است با:

${{\varphi }_{1}}=\frac{\pi }{6}rad$

از طرفی مدت زمان لازم برای این تغییر فاز از شروع حرکت تا نقطهٔ $N$، برابر $\Delta t=\frac{T}{12}$ می‌باشد (چرا؟). بنابراین می‌توان نوشت:

$\frac{T}{12}=2\Rightarrow T=24s$

گام دوم: در نقطهٔ $M$ مکان نوسانگر برابر ${{x}_{M}}=\frac{\sqrt{2}}{2}A$ بوده و جهت حرکت آن به سمت مرکز می‌باشد، بنابراین به یاد $\frac{\pi }{4}$ و مشتقات آن می‌افتیم:

${{\varphi }_{2}}=\frac{\pi }{4}rad$

گام سوم: تغییر فاز لازم برای جابه‌جایی از نقطهٔ $N$ تا $M$ برابر است با:

$\Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\frac{\pi }{4}-\frac{\pi }{6}=\frac{\pi }{12}rad$

از طرفی مدت زمان لازم برای تغییر فاز برابر $\Delta t=\frac{T}{24}$ می‌باشد و داریم:

خواستهٔ سؤال: $\Delta t=\frac{T}{24}=\frac{24}{24}=1s$