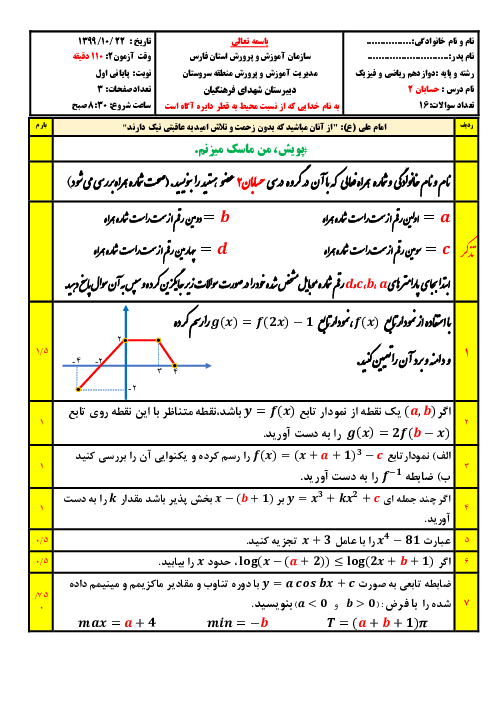
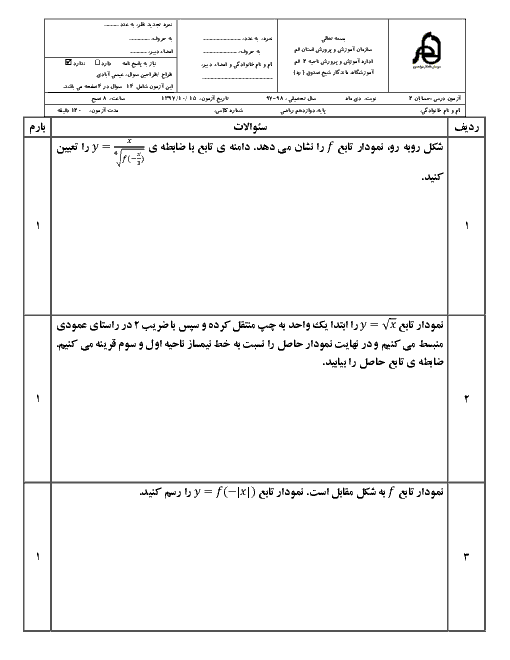
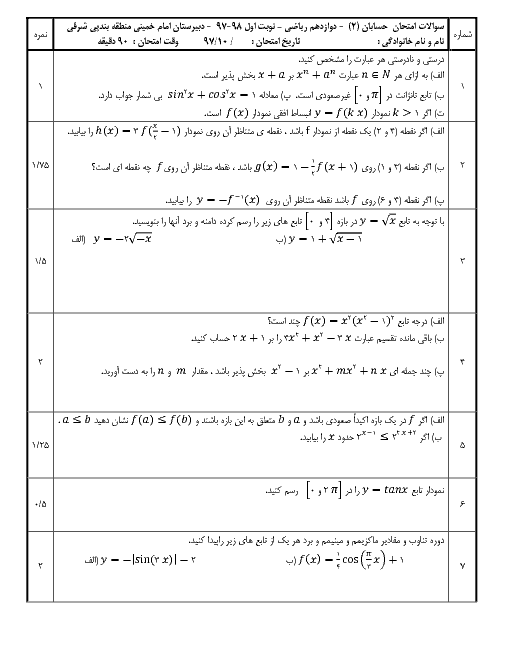
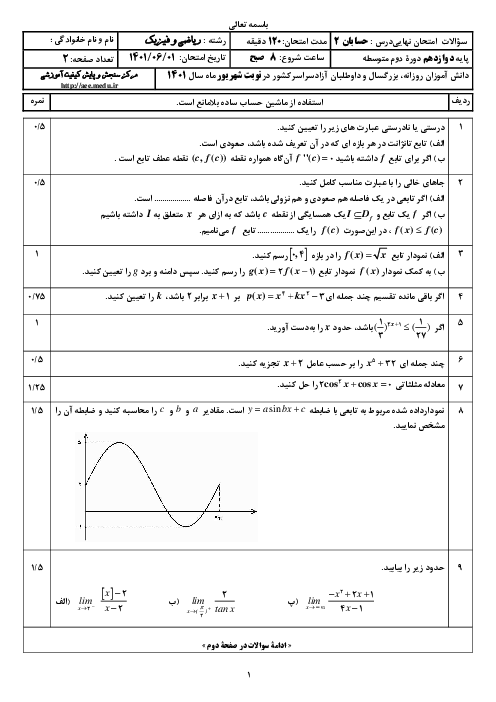
نکته: توابع $y=a\operatorname{Sin}bx+c$ و $y=a\operatorname{Cos}bx+c$ دارای مقدار ماکزیمم $\left| a \right|+c$ و مقدار مینیمم $-\left| a \right|+c$ و دورهٔ تناوب $\frac{2\pi }{\left| b \right|}$ هستند.
با توجه به نکته و تابع دادهشده داریم:
اختلاف ماکزیمم و مینیمم $=(c+\left| b \right|)-(c-\left| b \right|)=2\left| b \right|$
از طرفی دورهٔ تناوب تابع برابر است با: $T=\frac{2\pi }{\left| a \right|}$
بنابراین:
$2\left| b \right|=2\times \frac{2\pi }{\left| a \right|}\Rightarrow \left| a \right|\times \left| b \right|=2\pi \Rightarrow \left| ab \right|=2\pi $
با توجه به گزینهها، تنها گزینهٔ 3 در این شرط صدق میکند.