درس 3: اعمال بر روی توابع
ریاضی و آمار (2)
یازدهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
اگر تابع $\left( {\frac{f}{g}} \right)(x) = x - {x^2}$ و نمودار تابع $g(x)$ به صورت زیر باشد، ضابطهٔ تابع $f(x)$ را به دست آورید.
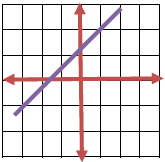
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!