درس 2: روابط تکمیلی بین نسبتهای مثلثاتی
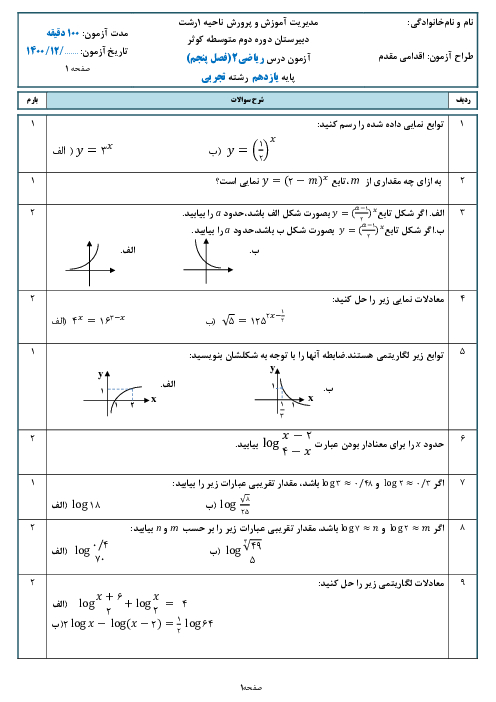
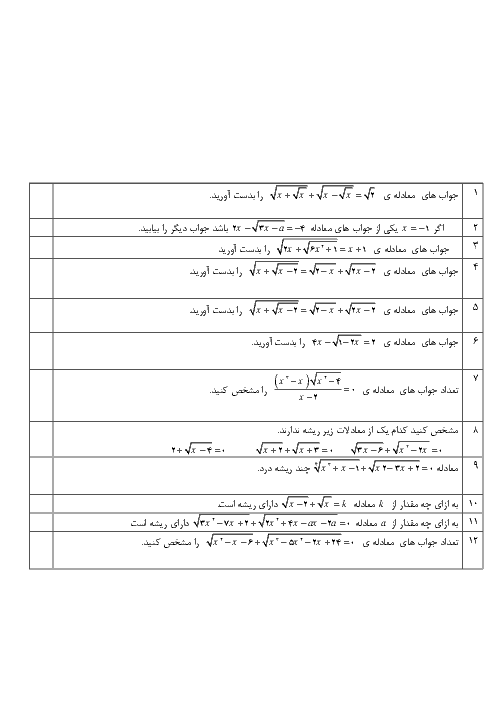
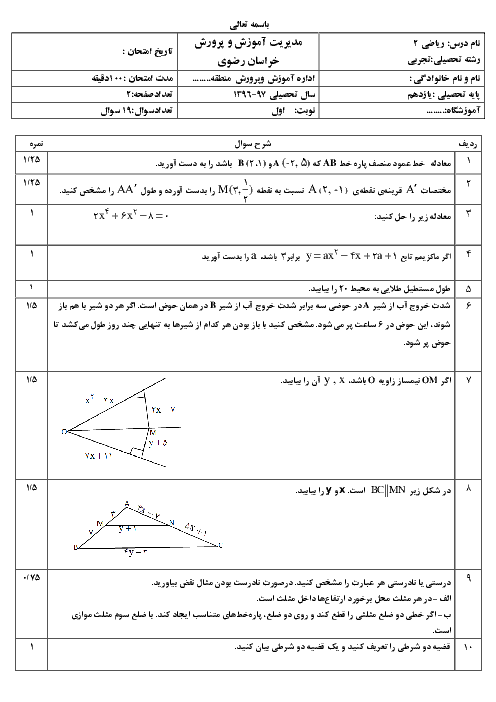
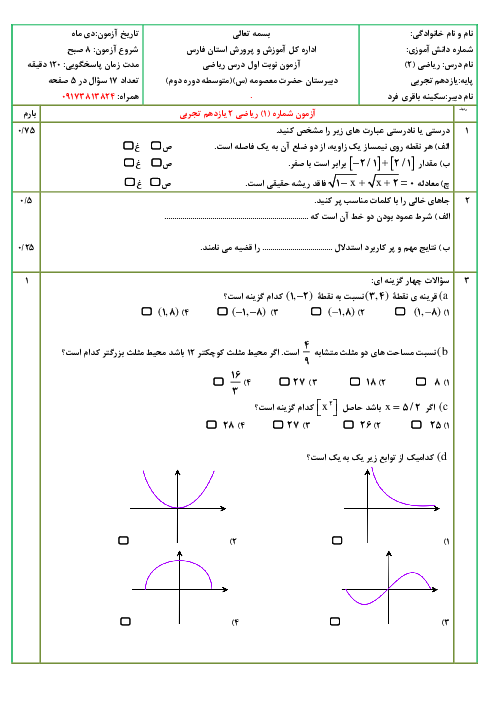
ریاضی (2)
یازدهم
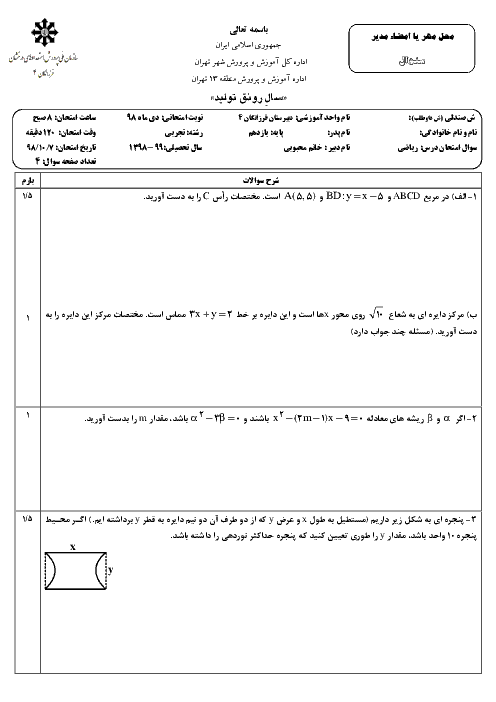
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر $\sin (2x+{{45}^{\circ }})=\cos ({{15}^{\circ }}-x)$، آنگاه کدام دو مقدار برای x در تساوی صدق میکند؟
1 )
60 درجه یا 420 درجه
2 )
30 درجه یا 300 درجه
390 درجه یا 380 درجه
4 )
20 درجه یا 340 درجه