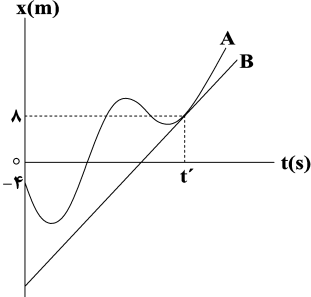
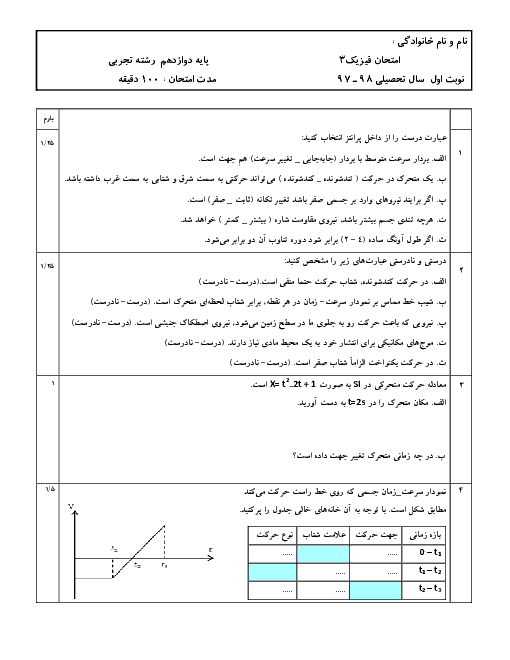
چون دو نمودار در لحظۀ ${t}'$ مماس بر یک‌دیگرند، پس سرعت آن‌ها در این لحظه با یک‌دیگر برابر است. با توجه به رابطۀ سرعت متوسط و شتاب متوسط، سرعت متحرک A را در لحظۀ ${t}'$ به‌ دست می‌آوریم:

$\begin{align}  & {{v}_{av}}=\frac{\Delta x}{\Delta t}\xrightarrow[\Delta t={t}',{{v}_{av}}=\frac{3}{2}\frac{m}{s}]{\Delta x=8-(-4)=12m}\frac{3}{2}=\frac{12}{{{t}'}}\Rightarrow {t}'=8s \\  & {{a}_{av}}=\frac{\Delta v}{\Delta t}\xrightarrow[{{v}_{0}}=-4\frac{m}{s},{t}'=8s]{\Delta v={{v}_{{{t}'}}}-{{v}_{0}},{{a}_{av}}=2\frac{m}{{{s}^{2}}}}2=\frac{{{v}_{{{t}'}}}+4}{8}\Rightarrow {{v}_{{{t}'}}}=12\frac{m}{s} \\ \end{align}$

اکنون با استفاده از رابطۀ مکان ـ زمان در حرکت یکنواخت، مکان اولیۀ متحرک B را به دست می‌آوریم:

$\begin{align}  & {{x}_{B}}={{v}_{B}}{t}'+{{x}_{0,B}}\Rightarrow 8=12\times 8+{{x}_{0,B}}\Rightarrow {{x}_{0,B}}=-88m \\  & \Rightarrow \Delta x={{x}_{0A}}-{{x}_{0B}}=84m \\ \end{align}$