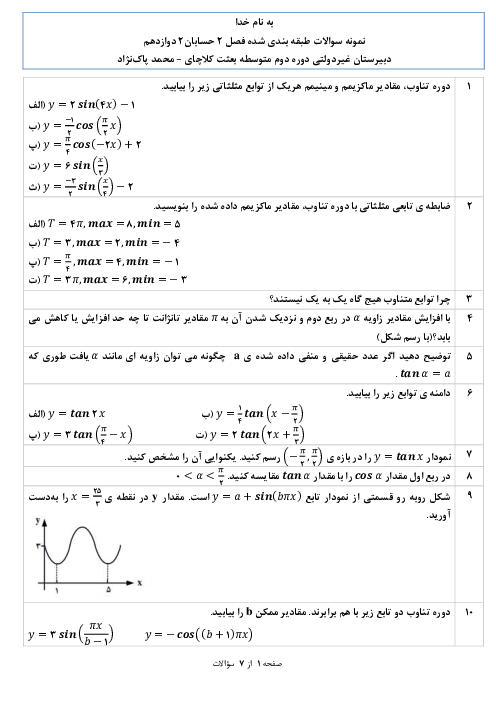
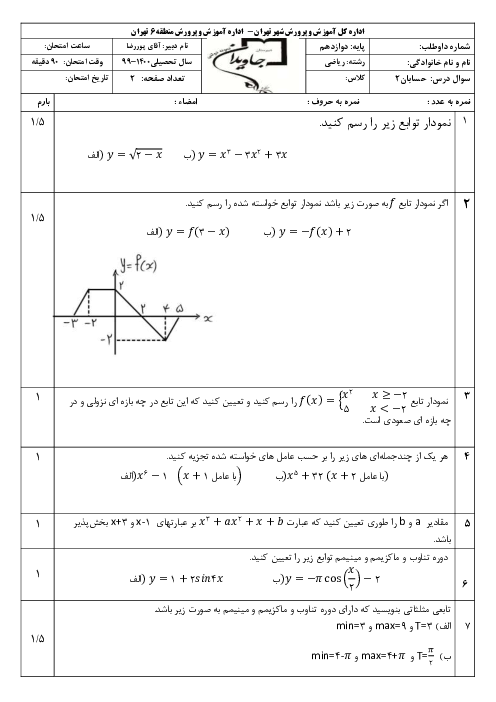
نكته: فرض كنيم تابع $f$ بر بازه‌ای مانند $(I\in {{D}_{f}})I$ پیوسته باشد و $c\in I$ یک نقطهٔ بحرانی تابع $f$ باشد. هر گاه $f$ بر این بازه به‌جز احتمالاً در نقطهٔ $c$، مشتق‌پذیر باشد، در این صورت:

الف) اگر به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(a,c)$، ${f}'(x)\gt 0$ و به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(c,b)$، ${f}'(x)\lt 0$، در اين صورت $f(c)$ يک مقدار ماكزيمم نسبی $f$ است.

ب) اگر به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(a,c)$، ${f}'(x)\lt 0$ و به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(c,b)$، ${f}'(x)\gt 0$، در اين صورت $f(c)$ يک مقدار مينيمم نسبی $f$ است.

پ) اگر ${f}'$ در نقطۀ $c$ تغيير علامت ندهد، به‌طوری كه ${f}'$ در هر دو طرف $c$ مثبت يا هر دو طرف آن منفی باشد، آنگاه $f(c)$ نه مينيمم نسبی و نه ماكزيمم نسبی است.

تابع $f$ مشتق‌پذير است و نقطۀ $A(2,-4)$ اكسترمم نسبی است. پس می‌توان نوشت: 

$\left\{ \begin{matrix} f(2)=-4\Rightarrow 2a+\frac{b}{2}=-4\Rightarrow 4a+b=-8  \\ {f}'(2)=0:{f}'(x)=a-\frac{b}{{{x}^{2}}}\Rightarrow {f}'(2)=0\Rightarrow a-\frac{b}{4} =0\Rightarrow b=4a  \\ \end{matrix} \right.\Rightarrow 8a=-8\Rightarrow a=-1,b=-4$

حال برای تعيين نوع اكسترمم نسبی، با استفاده از آزمون مشتق اول داريم: 

${f}'(x)=-1+\frac{4}{{{x}^{2}}}=\frac{4-{{x}^{2}}}{{{x}^{2}}}$

بنابراين نقطۀ $(2,-4)$ ماكزيمم نسبی تابع $f$ است و گزينۀ ۴ پاسخ است.