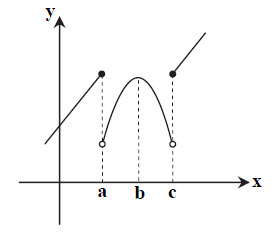
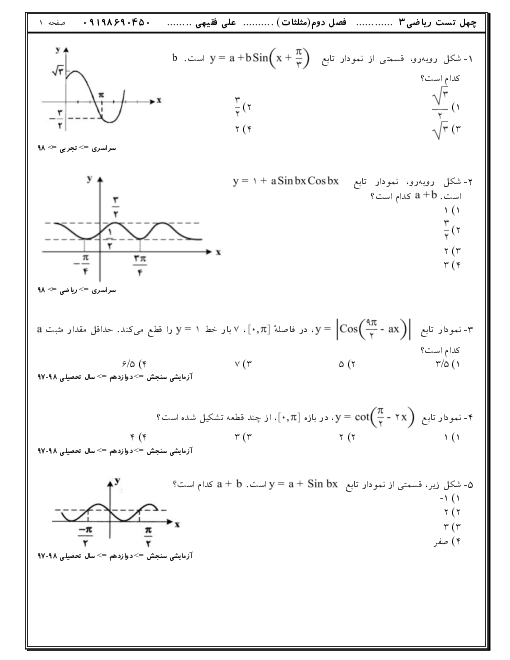
نكته: می‌گوييم تابع $f$ در نقطه‌ای به‌ طول $c$ ماكزيمم نسبی دارد، هرگاه يک همسايگی از $c$ مانند $I$ موجود باشد كه برای هر $x\in I$ داشته باشيم $f\left( c \right)\ge f\left( x \right)$، در اين حالت $f\left( c \right)$ مقدار ماكزيمم نسبی تابع $f$ ناميده می‌شود.

نكته: می‌گوييم تابع $f$ در نقطه‌ای به طول $c$ مينيمم نسبی دارد، هرگاه يک همسايگی از $c$ مانند $I$ موجود باشد كه برای هر $x\in I$ داشته باشيم $f\left( c \right)\le f\left( x \right)$ در اين حالت $f\left( c \right)$ را مقدار مينيمم نسبی تابع $f$ می‌ناميم.

با توجه به نكات بالا، تابع در $x=b,x=a$ ماكزيمم نسبی دارد، ولی تابع در $x=c$ اكسترمم نسبی ندارد؛ زيرا اگر يک همسايگی در اطراف $x=c$ در نظر بگيريم، داريم:

$\left\{ \begin{matrix}    x \gt c\Rightarrow f\left( x \right)\le f\left( c \right)  \\    x \lt c\Rightarrow f\left( x \right)\ge f\left( c \right)  \\ \end{matrix} \right.\Rightarrow x=c$