نکته: در معادله درجه دوم $a{{x}^{2}}+bx+c=0$، مجموع ریشه‌ها برابر $S=\frac{-b}{a}$ و حاصل ‌ضرب ريشه‌ها برابر $P=\frac{c}{a}$ است.

نکته: اگر ${{x}_{1}}$ و ${{x}_{2}}$ دو عدد حقيقی باشند، $S={{x}_{1}}+{{x}_{2}}$ و $P={{x}_{1}}{{x}_{2}}$ . آنگاه معادله‌ی درجه دومی كه ريشه‌های آن ${{x}_{1}}$ و ${{x}_{2}}$ باشد عبارت است از: ${{x}^{2}}-Sx+P=0$ 

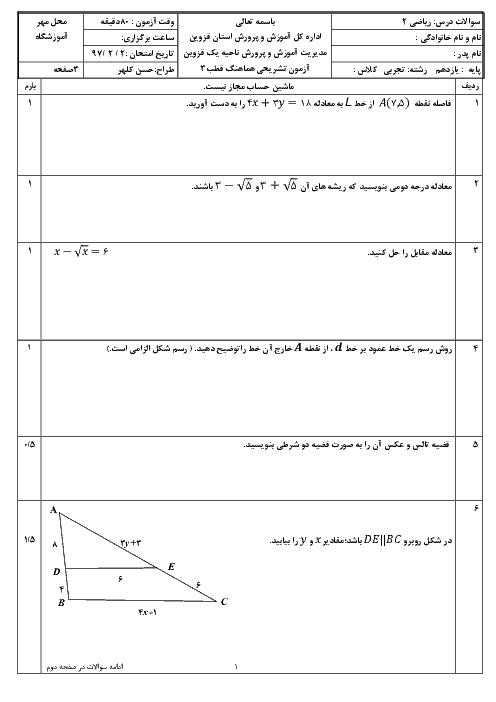
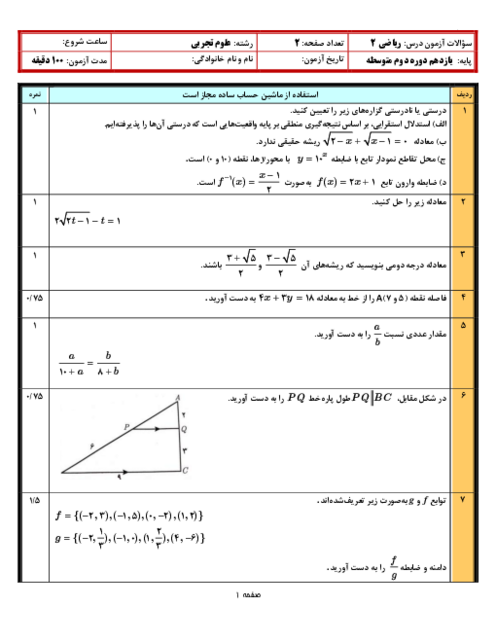
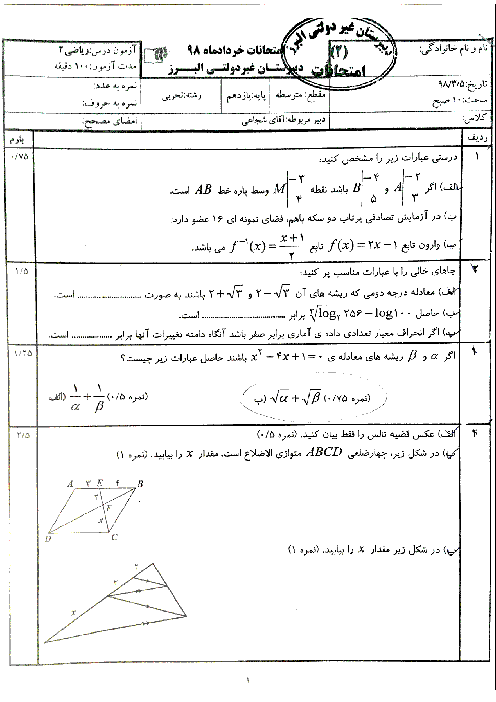
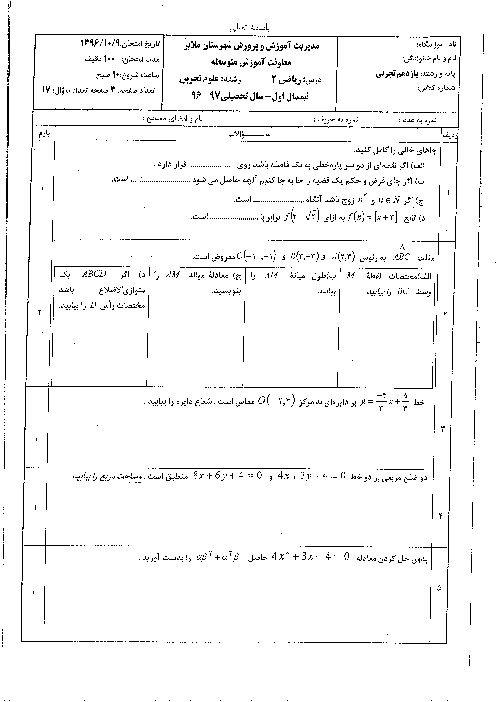
مجموع و حاصل ‌ضرب ريشه‌های معادله‌ی ${{x}^{2}}-3mx+4m-2=0$ برابر است با:

$S=3m,P=4m-2$ 

با جای‌ گذاری اين مقدار در رابطه‌ی $S+P=5$ داریم:

$3m+4m-2=0\Rightarrow 7m=7\Rightarrow m=1$ 

با جای ‌گذاری $m=1$، در معادله، به معادله‌ی ${{x}^{2}}-3x+2=0$ خواهیم رسید.

${{x}^{2}}-3x+2=0\Rightarrow (x-1)(x-2)=0\Rightarrow x=1,2\xrightarrow{{{x}_{1}}\langle {{x}_{2}}}{{x}_{1}}=1,{{x}_{2}}=2$ 

معادله‌ی درجه دومی كه ريشه‌های آن ${{x}_{2}}+2=4,{{x}_{1}}+1=2$ باشد عبارت است از: ${{x}^{2}}-6x+8=0$