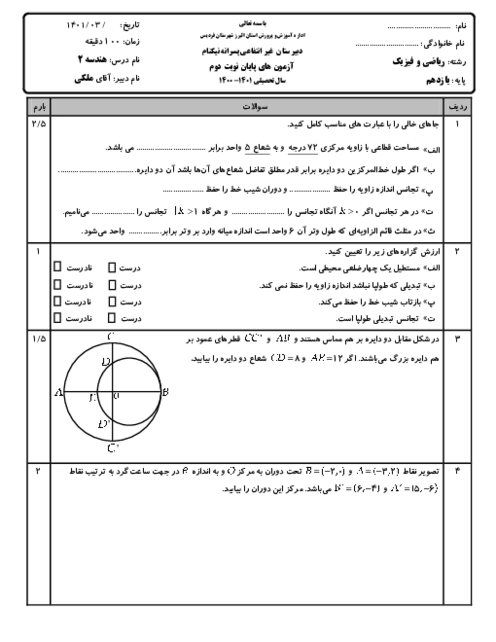
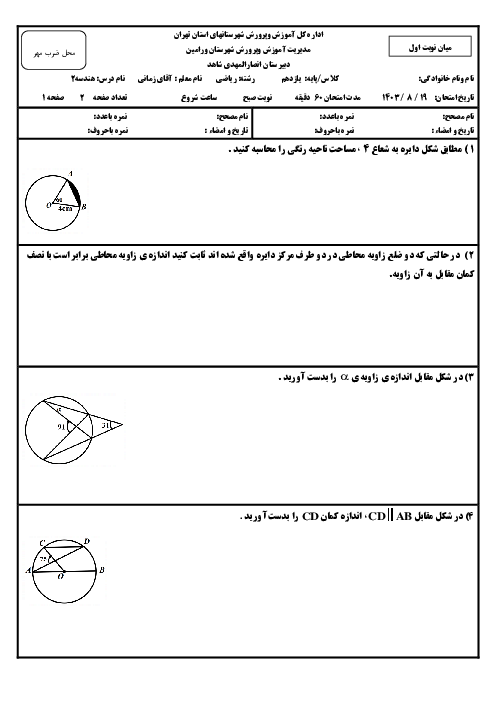
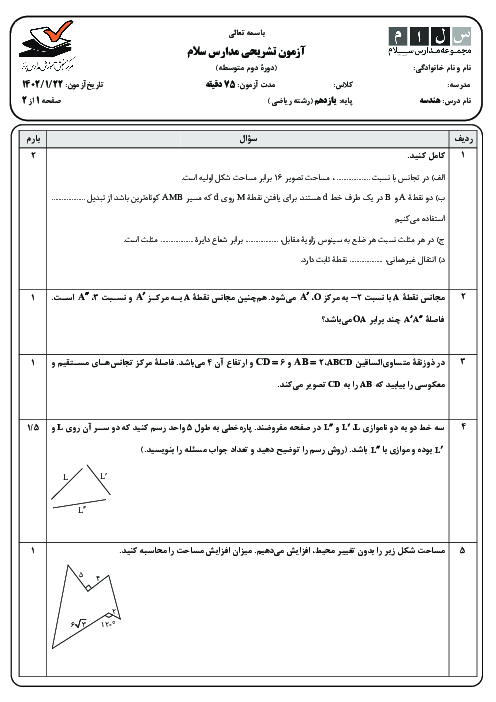
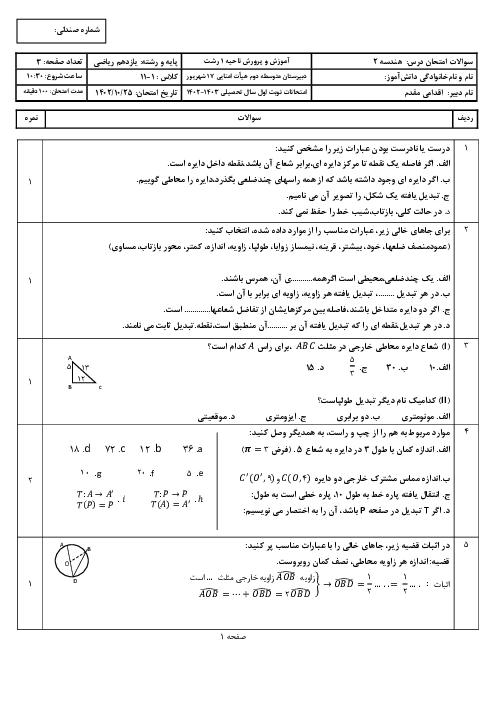
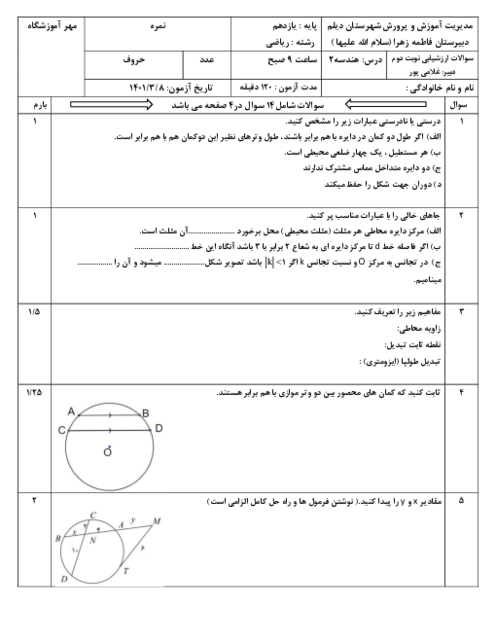
در مثلث ABC که ، و ، نقطهٔ M وسط ضلع BC است. محیط مثلث AMC را به‌دست آورید. | هندسه (2) یازدهم شماره 331400 - گاما

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 2: قضیۀ کسینوس‌ها هندسه (2) یازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در مثلث ABC که $AB=4$، $AC=6$ و $BC=8$، نقطهٔ M وسط ضلع BC است. محیط مثلث AMC را به‌دست آورید.

نمایش پاسخ

${6^2} + {4^2} = 2A{M^2} + \frac{{{8^2}}}{2} \to 36 + 16 = 2A{M^2} + 32$
$ \to A{M^2} = 10 \to AM = \sqrt {10} $
$ \to 2{P_{AMC}} = 6 + 4 + \sqrt {10} = 10 + \sqrt {10} $

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

تحلیل ویدئویی برای این تست ثبت نشده است!

ویدیو دوره آموزشی، هندسه (2) یازدهم دوره دوم متوسطه- نظری

مدرس: محمد بادپا

مدت دوره: 7 ساعت (14 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

سوپراستار

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 2 یازدهم رشته ریاضی فیزیک

51 صفحه

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 2 یازدهم رشته ریاضی فیزیک

کلاس یازدهمی

رایـــــگان

نمونه سوال امتحان نوبت اول هندسه (2) پایه یازدهم رشته ریاضی | ویژه دی 96

1 صفحه

نمونه سوال امتحان نوبت اول هندسه (2) پایه یازدهم رشته ریاضی | ویژه دی…

کلاس یازدهمی

آزمون هندسه (2) یازدهم دبیرستان شیخ فضل الله نوری | روابط زاویه‌ها و رابطه‌های طولی در دایره

6 صفحه

آزمون هندسه (2) یازدهم دبیرستان شیخ فضل الله نوری | روابط زاویه‌ها و رابطه‌های…

محمدجواد باغبان باشی

سوالات امتحان نوبت اول هندسه (2) یازدهم دبیرستان رحمت | دی 1399

2 صفحه

سوالات امتحان نوبت اول هندسه (2) یازدهم دبیرستان رحمت | دی 1399

فاطمه رحیمی

سوال و پاسخ امتحان ترم اول هندسه (2) یازدهم دبیرستان امام خمینی | دی 97

3 صفحه

سوال و پاسخ امتحان ترم اول هندسه (2) یازدهم دبیرستان امام خمینی | دی 97

اسماعیل ادبی فیروزجایی

رایـــــگان

سوالات امتحانات ترم اول هندسه یازدهم مدارس سرای دانش | دی 98

22 صفحه

سوالات امتحانات ترم اول هندسه یازدهم مدارس سرای دانش | دی 98

سرای دانش

آزمون میان‌ترم هندسه 2 سال یازدهم دبیرستان وارثان حسین | فصل 1 (درس 1 و 2 و 3)

2 صفحه

آزمون میان‌ترم هندسه 2 سال یازدهم دبیرستان وارثان حسین | فصل 1 (درس 1…

علیرضا شریفی

نمونه سوال امتحان نوبت دوم هندسه یازدهم | خرداد 1397

5 صفحه

نمونه سوال امتحان نوبت دوم هندسه یازدهم | خرداد 1397

فائزه ربیعی

سوالات امتحان فصل 1: دایره | میان ترم اول هندسه یازدهم

4 صفحه

سوالات امتحان فصل 1: دایره | میان ترم اول هندسه یازدهم

مجتبی زمانی

آزمون نوبت دوم هندسه (2) یازدهم هماهنگ مدارس خارج از کشور | دی 1397

2 صفحه

آزمون نوبت دوم هندسه (2) یازدهم هماهنگ مدارس خارج از کشور | دی 1397

محبوبه نیازی

موارد بیشتر

موارد بیشتر

ارسال فایل

در شکل زیر مقدار a کدام است؟

صحیح یا غلط بودن عبارت زیر را تعیین کنید.

فاصله‌ی نقاط دایره تا نقطه p را به دست آورید.

موارد بیشتر

ارسال پرسش

موارد بیشتر