درس 2: حل معادلۀ درجۀ 2 و کاربردها
ریاضی و آمار (1)
دهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
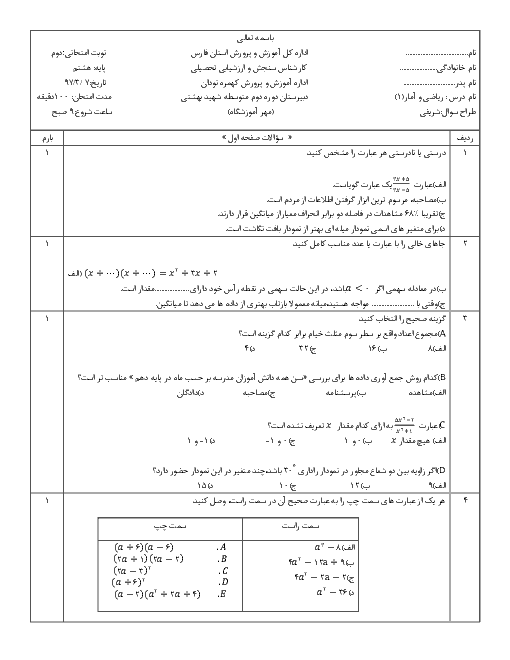
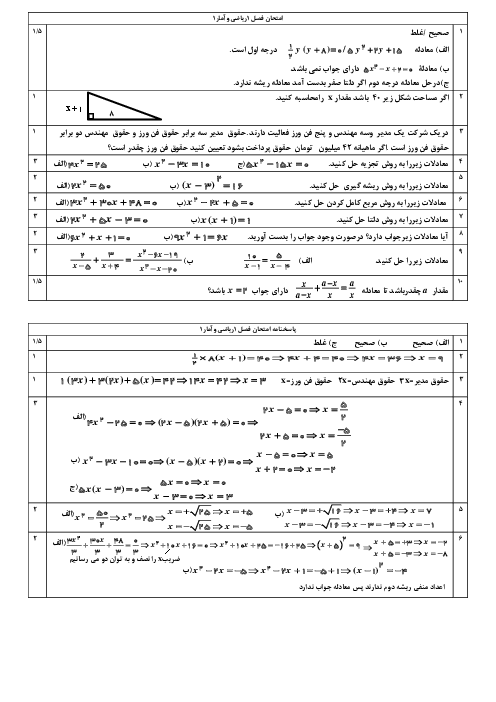
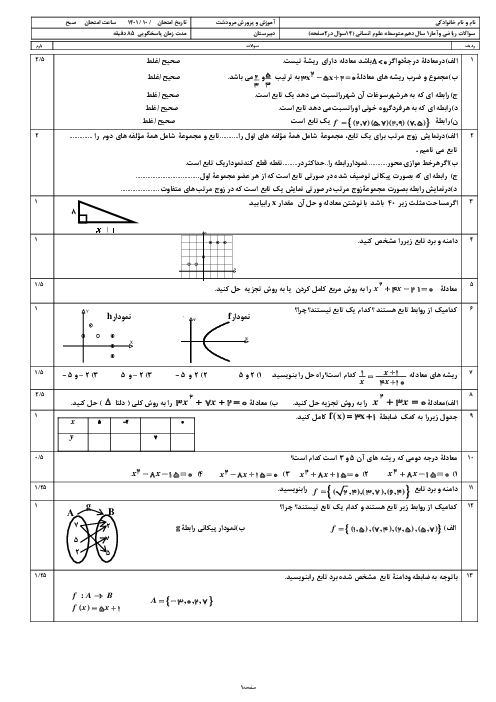
در مورد ریشه‌های معادلهٔ ${(\frac{{{x^2}}}{2} + 7)^2} - 9(\frac{{{x^2}}}{2} + 7) = 0$ چه می‌توان گفت؟
1 )
دارای یک ریشهٔ مضاعف و دو ریشهٔ قرینه می‌باشد.
2 )
دارای چهار ریشه می‌باشد که شامل دو جفت ریشهٔ قرینه است.
دارای دو ریشهٔ قرینه است.
4 )
فاقد ریشهٔ حقیقی است.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...