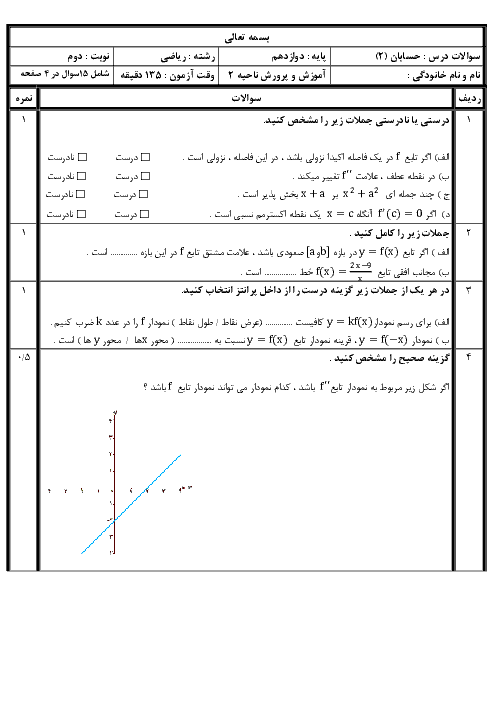
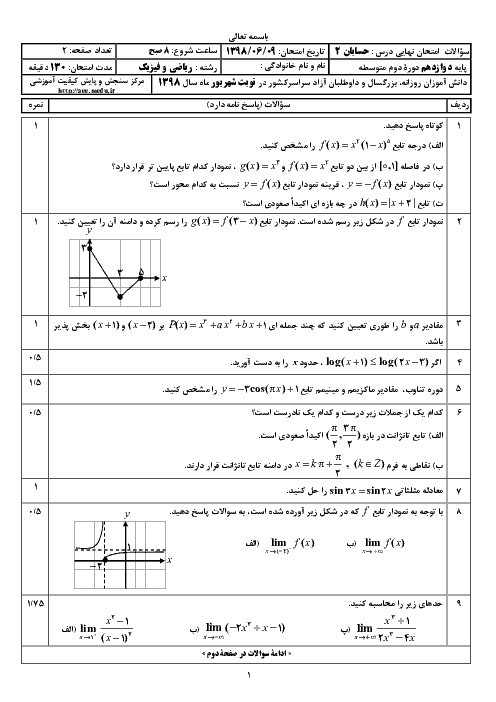
برای مشتقپذیر بودن تابع در $x=\frac{\pi }{2}$ اولاً باید تابع در این نقطه پیوسته باشد، ثانیاً باید مشتق چپ و راست تابع در این نقطه برابر باشند.
$f(x)=\left\{ \begin{matrix} \cos x\,\,\,\,\,;x\le \frac{\pi }{2} \\ ax-b\,\,\,\,\,;x \gt \frac{\pi }{2} \\ \end{matrix} \right.$
$\underset{x\to {{\frac{\pi }{2}}^{+}}}{\mathop{\lim }}\,f(x)=a\frac{\pi }{2}-b\,\,,\,\,\underset{x\to {{\frac{\pi }{2}}^{-}}}{\mathop{\lim }}\,f(x)=f\left( \frac{\pi }{2} \right)=0\Rightarrow \frac{a\pi }{2}-b=0\,\,\,(1)$
${ f}'(x)=\left\{ \begin{matrix} -\sin x\,\,\,\,\,;x \lt \frac{\pi }{2} \\ a\,\,\,\,\,\,\,\,\,\,\,\,\,;x \gt \frac{\pi }{2} \\ \end{matrix} \right.$
${{{f}'}_{-}}\left( \frac{\pi }{2} \right)=-\sin \frac{\pi }{2}=-1\,\,,\,\,{{{f}'}_{+}}\left( \frac{\pi }{2} \right)=a\Rightarrow a=-1$
$(1)\,\frac{a\pi }{2}-b=0\Rightarrow -\frac{\pi }{2}-b=0\Rightarrow b=-\frac{\pi }{2}$