درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در تابع $f(x)=\left\{ \begin{matrix}{{x}^{2}};x\ge -1 \\ 2;x<-1 \\\end{matrix} \right.$، اگر برای هر دو مقدار $a$ و $b$ در بازهٔ $\left( -1,0 \right)$ داشته باشیم: $a \lt b$، آن گاه کدام مورد همواره صحیح است؟
1 )
$f(a) \lt f(b)$
$f({{a}^{2}}) \gt f({{b}^{2}})$
3 )
$f(a)-f(b)\left| \lt \right|\left. a-b \right|$
4 )
$f(a)+f(b) \gt \left| a \right|+\left| b \right|$
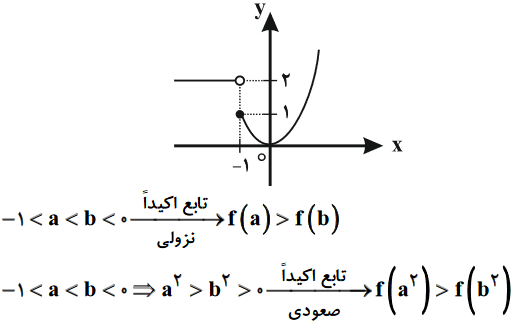
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...