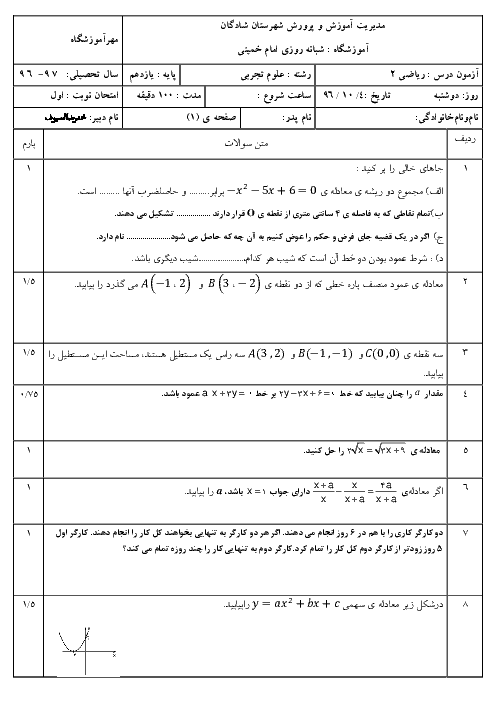
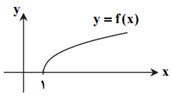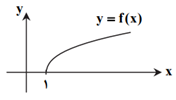نكته: فرض كنيم $f(x)$ در بازه‌ای مانند $(a,{{x}_{0}})$ تعريف‌ شده باشد؛ می‌گوييم حد چپ $f(x)$ در $x={{x}_{0}}$ برابر $\ell $ است و می‌نویسیم $\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f(x)=\ell $، هرگاه بتوان مقادیر $f(x)$ را به اندازهٔ دلخواه به $\ell $ نزديک كرد، به ‌شرطی كه مقادير $X$ از سمت چپ به‌اندازهٔ كافی به ${{x}_{0}}$ نزدیک شوند.

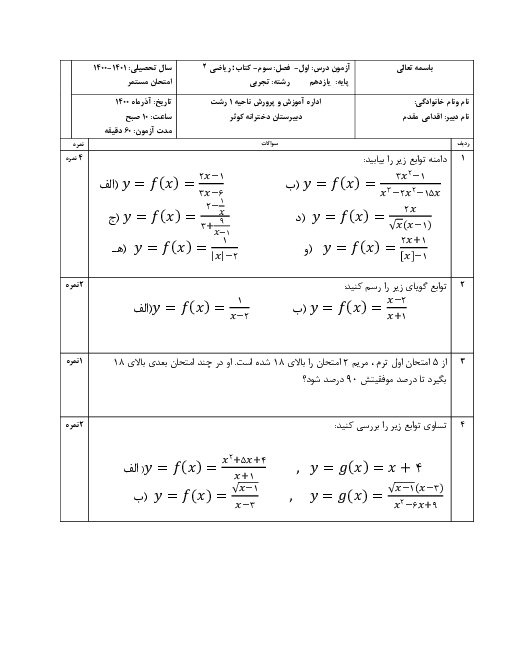
نكته: فرض كنيم $f(x)$ در بازه‌ای مانند $({{x}_{0}},b)$ تعريف ‌شده باشد؛ می‌گوييم حد راست $f(x)$ در $x={{x}_{0}}$ برابر $\ell $ است و می‌نویسیم $\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f(x)=\ell $، هرگاه بتوان مقادیر $f(x)$ را به اندازهٔ دلخواه به $\ell $ نزديک كرد، به‌ شرطی كه مقادير $X$ از سمت راست به‌اندازهٔ كافی به ${{x}_{0}}$ نزدیک شوند.

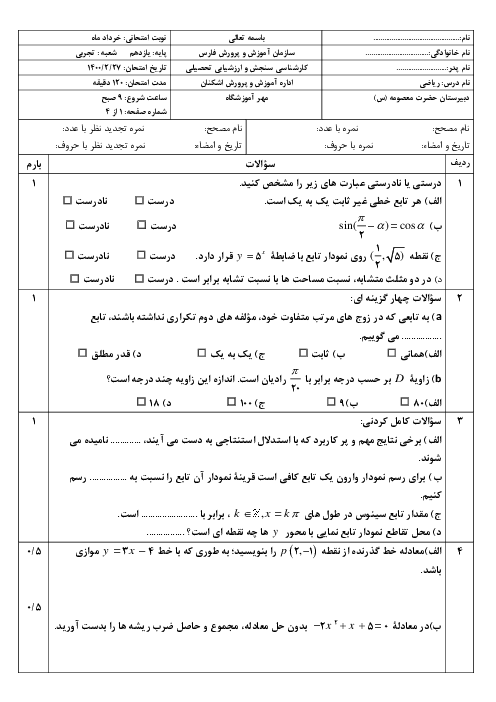
نكته: فرض كنيم $f(x)$ در بازه‌ای مانند $(a,b)$ شامل ${{x}_{0}}$ (به‌جز احتمالاً در خود ${{x}_{0}}$) تعريف‌شده باشد؛ می‌گوييم حد تابع $f(x)$ در $x={{x}_{0}}$ برابر $\ell $ است و می‌نویسیم $\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=\ell $، هرگاه بتوان مقادیر $f(x)$ را به اندازهٔ دلخواه به $\ell $ نزديک كرد، به‌شرطی كه مقادير $X$ (از سمت چپ و راست) به‌اندازهٔ كافی به ${{x}_{0}}$ نزدیک شوند؛ به عبارت دیگر $\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f(x)=\ell $، اگر و تنها اگر $\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f(x)=\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f(x)=\ell $.

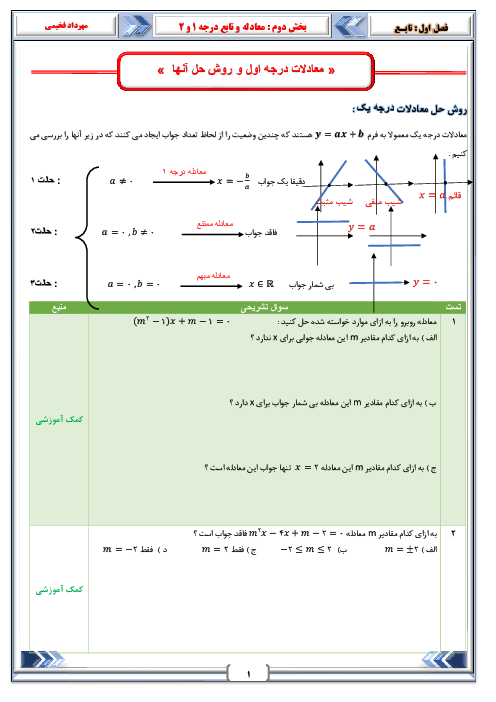
با توجه به‌شكل مقابل می‌توان فهميد $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)$ و در نتیجه $\underset{x\to 1}{\mathop{\lim }}\,f(x)$ وجود ندارد، همچنین $\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)$ موجود نیست؛ ولی داریم:

$f(1)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)=0$