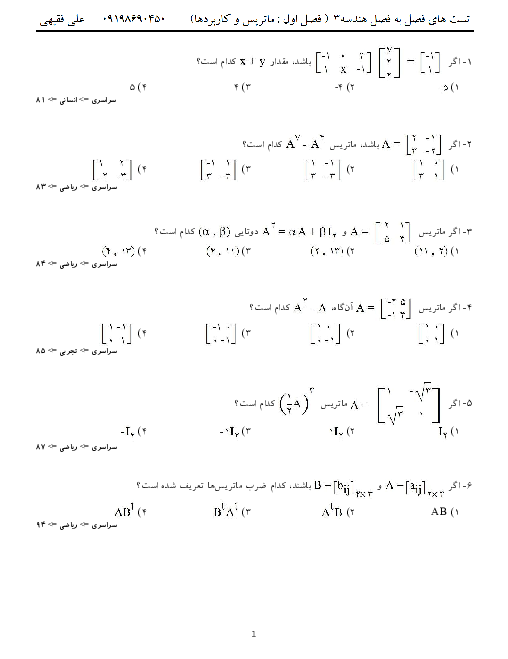
نكته: زاويۀ بين دو بردار $a$ و $b$ به‌صورت روبه‌رو است: $\operatorname{Cos}\alpha =\frac{a.b}{\left| a \right|\left| b \right|}$

ابتدا بردارهای $a$ و $b$ را به‌دست می‌آوریم:

$\left\{ \begin{matrix} \overrightarrow{a}=2\overrightarrow{i}+\overrightarrow{j}+\overrightarrow{k}=(2,1,1)  \\ \overrightarrow{b}=\overrightarrow{k}-\overrightarrow{j}=(0,-1,1)  \\ \end{matrix} \right.$

قطرهای متوازی‌الاضلاع بناشده بر دو بردار $a$ و $b$ بردارهای $a+b$ و $a-b$ است:

$\left\{ \begin{matrix} \vec{a}+\overrightarrow{b}=(2,0,2)  \\ \vec{a}-\vec{b}=(2,2,0)  \\ \end{matrix} \right.$

بنابراین مطابق نکته داریم:

$\operatorname{Cos}\alpha =\frac{(\overrightarrow{a}+\overrightarrow{b}).(\overrightarrow{a}-\overrightarrow{b})}{\left| \overrightarrow{a}+\overrightarrow{b} \right|\left| \overrightarrow{a}-\overrightarrow{b} \right|}=\frac{4+0+0}{\sqrt{4+4}\times \sqrt{4+4}}\Rightarrow \operatorname{Cos}\alpha =\frac{4}{8}=\frac{1}{2}\Rightarrow \hat{\alpha }=\frac{\pi }{3}$