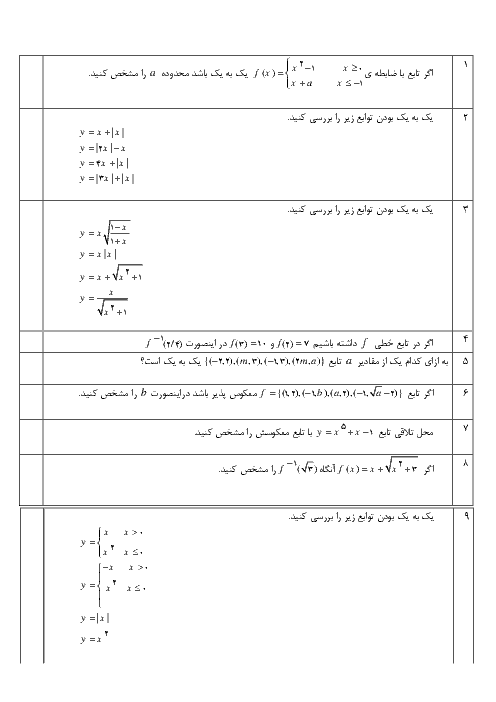
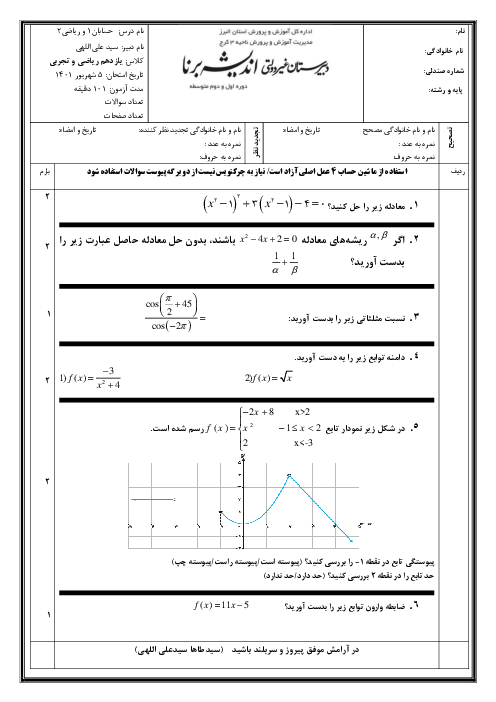
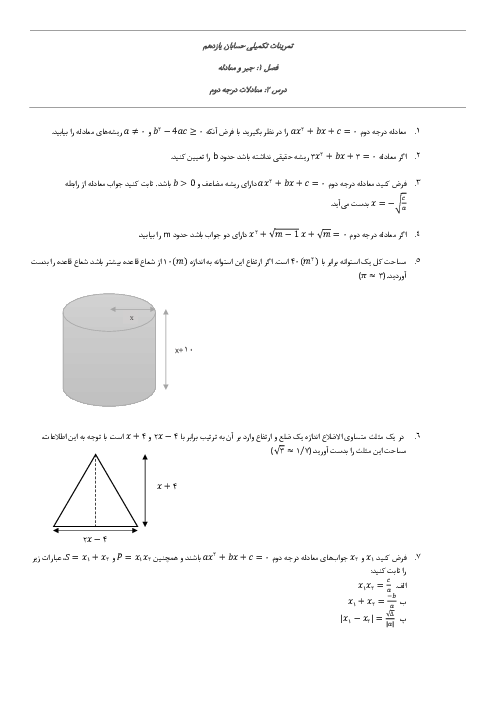
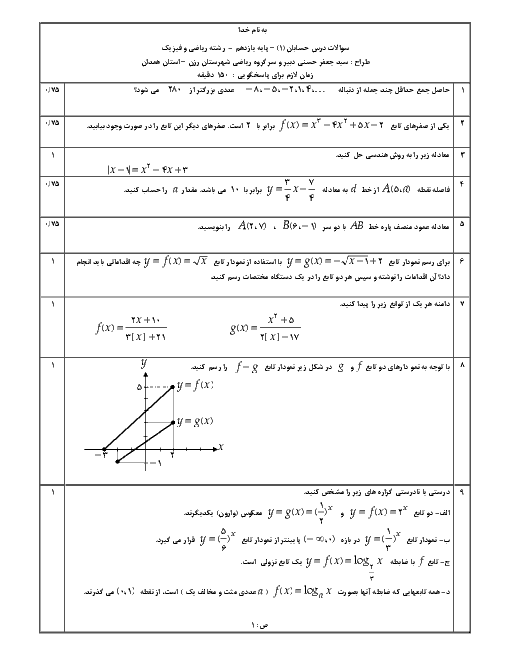
مساحت و محیط مربعی که دو ضلع آن روی خطهای $2x - y = 3$ و $4x - 2y + 7 = 0$ قرار دارد را بیابید.
پاسخ تشریحی :
$\eqalign{
& 2x - y = 3 \to 2x - y - 3 = 0 \to m = \frac{{ - 2}}{{ - 1}} = 2 \cr
& 4x - 2y + 7 = 0 \to m = \frac{{ - 4}}{{ - 2}} = 2 \cr} $
پس دو خط با هم موازی هستند یعنی دو ضلع روبهروی هم هستند. در نتیجه فاصله این دو خط طول ضلع مربع خواهد بود: (شکل)
فاصله دو خط موازی از رابطه زیر به دست میآید:
$AB = \frac{{\left| {c - c'} \right|}}{{\sqrt {{a^2} + {b^2}} }} \to AB = \frac{{\left| {7 - 3} \right|}}{{\sqrt {{4^2} + {2^2}} }} = \frac{{\left| 4 \right|}}{{\sqrt {16 + 4} }} = \frac{4}{{\sqrt {20} }} = \frac{4}{{2\sqrt 5 }} = \frac{2}{{\sqrt 5 }}$
حالا مساحت مربع را محاسبه میکنیم:
$s = {(AB)^2} = {\left( {\frac{4}{{\sqrt {20} }}} \right)^2} = \frac{{16}}{{20}} = \frac{4}{5}$
محیط مربع را به دست میآوریم:
$P = 4AB = 4\frac{2}{{\sqrt 5 }} = \frac{8}{{\sqrt 5 }}$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!