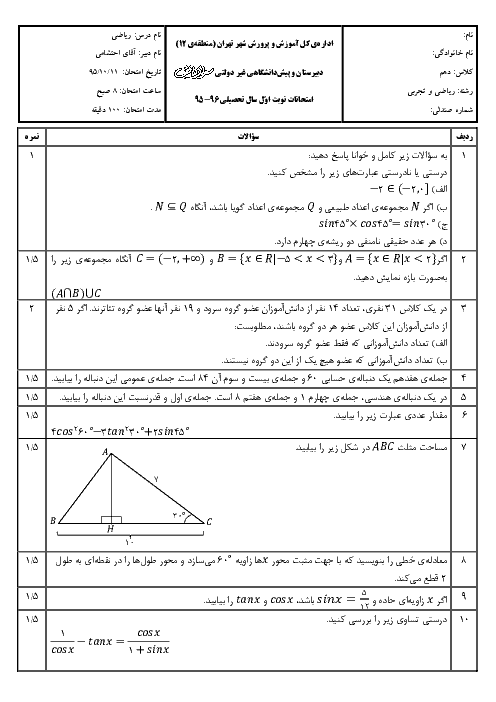
اعداد آخر هر دسته دنباله‌ای به صورت زیر می‌باشند:

${a_n}:\,\,\,\,\,1,3,6,12,24, \cdots $

از جمله دوم به بعد تشکیل دنباله هندسی با جمله اول 3 و قدر نسبت 2 به صورت زیر می‌دهند:

${b_n}:\,\,\,\,3,6,12,24, \cdots $

جمله آخر دسته دوازدهم:  ${a_{12}} = {b_{11}} = 3 \times {2^{10}} = 3072$

جمله اول دسته سیزدهم:   $3073$

جمله آخر دسته سیزدهم:    ${a_{13}} = {b_{12}} = 3 \times {2^{11}} = 6144$

اعداد دسته سیزدهم تشکیل دنباله حسابی با قدر نسبت 1 می‌دهند و مجموع آن‌ها از فرمول زیر بدست می‌آیند

$\frac{{n({c_1} + {c_n})}}{2}$

پس میانگین آنها به از فرمول زیر بدست می‌آیند:

$\frac{{\frac{{n({c_1} + {c_n})}}{2}}}{n} = \frac{{{c_1} + {c_n}}}{2}$

در واقع میانگین دسته سیزدهم از جمع جمله اول و آخر تقسیم بر دو به دست می‌آید و لذا:

$\overline X  = \frac{{3073 + 6144}}{2} = 4608/5$