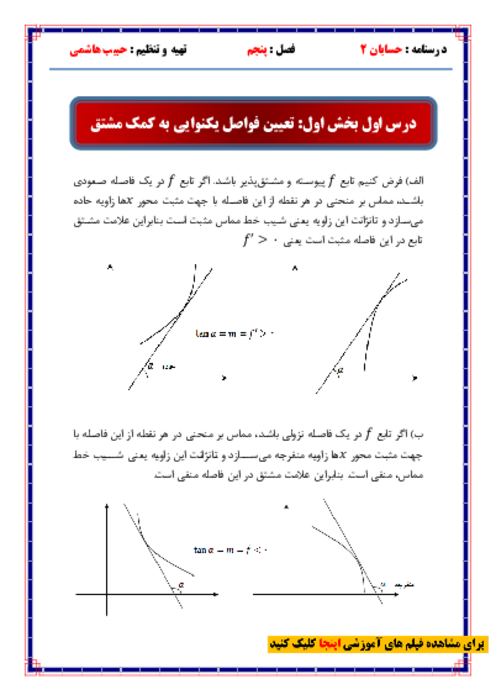
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر تابعهایی به صورت $f(x)={{x}^{3}}-(m+2){{x}^{2}}+3x$ همواره صعودی باشند، آنگاه مجموعه طول نقاط عطف این تابع، در کدام بازه است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!