درس 3: تابع نمایی
ریاضی و آمار (3)
دوازدهم
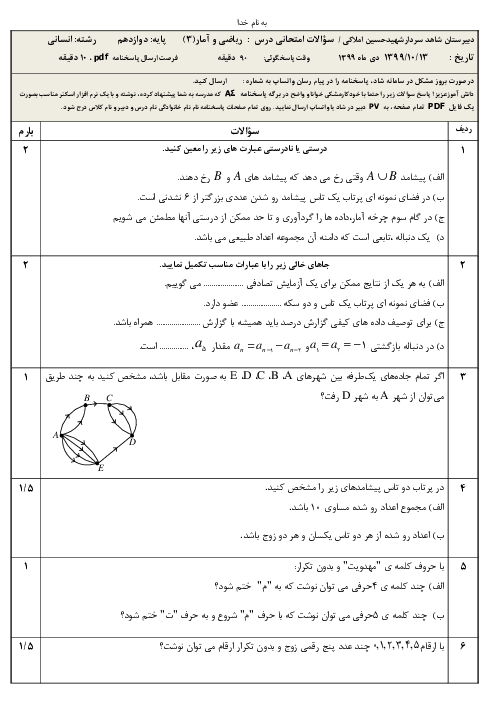
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
اگر ضابطۀ تابع نمایی به صورت $f\left( x \right)={{3}^{-x+2}}$ باشد، حاصل $f\left( -2+x \right)+3f\left( x+1 \right)$ کدام است؟
1 )
$9\times {{3}^{x}}$
$10\times {{3}^{2-x}}$
3 )
$9\times {{3}^{x-2}}$
4 )
$10\times {{3}^{x-2}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...