نمودارهای انرژی پتانسیل و انرژی جنبشی نوسانگر جرم ـ فنری در یک حرکت هماهنگ ساده به صورت شکل زیر است. وقتی نوسانگر از مکان تا مکان x = 0 جابه‌جا می‌شود، به اندازۀ… | فیزیک (3) تجربی دوازدهم شماره 225797

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 3: نوسان و امواج فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

نمودارهای انرژی پتانسیل و انرژی جنبشی نوسانگر جرم ـ فنری در یک حرکت هماهنگ ساده به صورت شکل زیر است. وقتی نوسانگر از مکان $x = {x_1}$ تا مکان x = 0 جابه‌جا می‌شود، به اندازۀ $8\frac{m}{s}$ به تندی آن افزوده می‌گردد. تندی نوسانگر هنگام عبور از مکان x = 0 چند متر بر ثانیه است؟ $(\sqrt 2 = 1/4)$

1 )

2 )

3 )

4 )

نمایش پاسخ

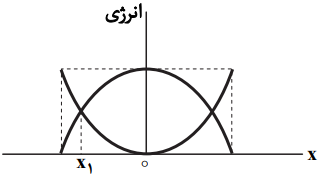
همان‌طور که شکل نشان می‌دهد، در مکان $x = {x_1}$ انرژی پتانسیل و انرژی جنبشی با هم برابر است و هر یک نصف انرژی مکانیکی خواهد بود. از طرفی انرژی مکانیکی نوسانگر با بیشینۀ انرژی جنبشی نوسانگر برابر است.

${U_1} + {K_1} = E \Rightarrow {K_1} + {K_1} = E \Rightarrow 2(\frac{1}{2}mv_1^2) = \frac{1}{2}mv_{\max }^2 \Rightarrow {v_1} = \frac{1}{{\sqrt 2 }}{v_{\max }}$

وقتی نوسانگر از $x = {x_1}$ به x = 0 می‌رسد، تندی آن از ${v_1} = \frac{{{v_{\max }}}}{{\sqrt 2 }}$ به ${v_{\max }}$ خواهد رسید؛ پس:

$\frac{{{v_{\max }}}}{{\sqrt 2 }} + 8 = {v_{\max }} \Rightarrow 8 = {v_{\max }} - \frac{{{v_{\max }}}}{{1/4}} \Rightarrow {v_{\max }} = 28\frac{m}{s}$

گزارش اشکال