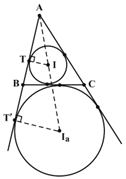
$I$ و ${{I}_{a}}$ هر دو روی نيمساز داخلی زاويهٔ A قرار دارند، پس $A$، $I$ و ${{I}_{a}}$ روی يک خط می‌باشند. از مماس بودن دايره‌ها بر اضلاع نتيجه می‌گیریم:

$\left. \begin{matrix} I\hat{T}A={{I}_{a}}{\hat{T}}'A={{90}^{{}^\circ }}  \\ I\hat{A}T={{I}_{a}}\hat{A}{T}'  \\ \end{matrix} \right\}\xrightarrow{}A\overset{\Delta }{\mathop{T}}\,I\sim A\overset{\Delta }{\mathop{{{T}'}}}\,{{I}_{a}}$

$\Rightarrow \frac{AI}{A{{I}_{a}}}=\frac{IT}{{{I}_{a}}{T}'}=\frac{r}{{{r}_{a}}}$   (1)

و از طرفی می‌دانيم:

$\left. \begin{matrix} S=rp\Rightarrow r=\frac{S}{p}  \\ {{r}_{a}}=\frac{S}{p-a}  \\ \end{matrix} \right\}\Rightarrow \frac{r}{{{r}_{a}}}=\frac{\frac{S}{p}}{\frac{S}{p-a}}=\frac{p-a}{p}$    (2)

بنابراين طبق روابط (1) و (2) داريم: 

$\frac{AI}{A{{I}_{a}}}=\frac{p-a}{p}\to \frac{AI}{I{{I}_{a}}}=\frac{p-a}{a}$