قسمت 3: حرکت با شتاب ثابت
فیزیک (3) ریاضی
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
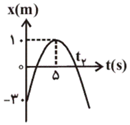
نمودار مکان - زمان متحرکی که با شتاب ثابت بر روی خط راست حرکت میکند، مطابق شکل زیر است. اندازهی شتاب متحرک و زمان ${{t}_{2}}$ در $SI$ بهترتیب از راست به چپ کداماند؟