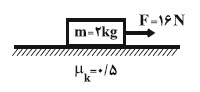
در ابتدا با استفاده از قانون دوم نيوتون، شتاب حركت جسم در حضور نيروی $\overrightarrow{F}$ را می‌یابیم.

$a=\frac{{{F}_{net}}}{m}\Rightarrow a=\frac{F-{{f}_{k}}}{m}=\frac{F-{{\mu }_{k}}mg}{m}=\frac{16-0/5\times 2\times 10}{2}\Rightarrow a=3\frac{m}{{{s}^{2}}}$

حال سرعت جسم را در لحظۀ قطع نیروی $\overrightarrow{F}$ محاسبه می‌کنیم:

$v=at+{{v}_{0}}=3\times 2+0\Rightarrow v=6\frac{m}{s}$

بعد از قطع نيروی $\overrightarrow{F}$ جسم با شتاب ${a}'$ حرکت می‌کند که برابر است با:

$\overrightarrow{{{a}'}}=\frac{{{\overrightarrow{F}}^{\prime }}_{net}}{m}\Rightarrow {a}'=\frac{-{{f}_{k}}}{m}\Rightarrow {a}'=\frac{-{{\mu }_{k}}mg}{m}\Rightarrow {a}'=-{{\mu }_{k}}g=-0/5\times 10\Rightarrow {a}'=-5\frac{m}{{{s}^{2}}}$

و برای پيدا كردن سرعت جسم در لحظۀ $t=3s$ (یعنی یک ثانیه بعد از قطع نیروی $\overrightarrow{F}$)، داریم:

${v}'=at+v=-5\times 1+6\Rightarrow {v}'=1\frac{m}{s}$

بنابراین در این لحظه داریم:

$p=m{v}'=2\times 1\Rightarrow p=2\frac{kg.m}{s}$