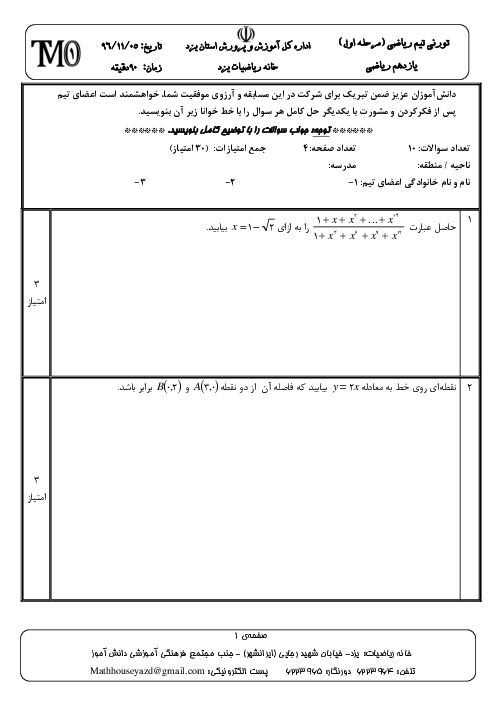
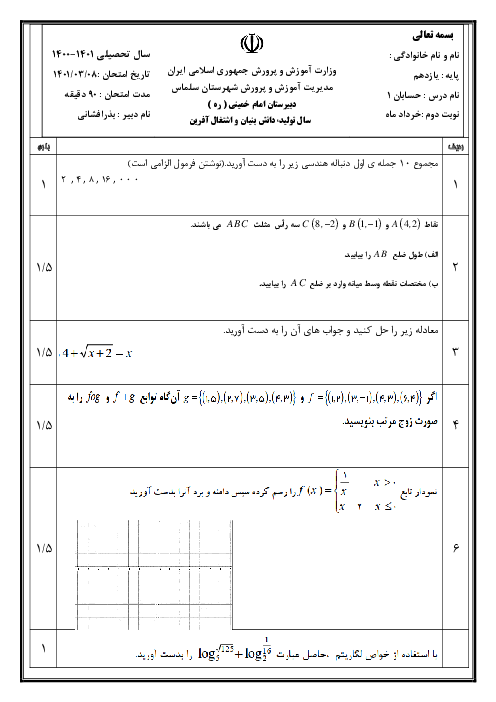
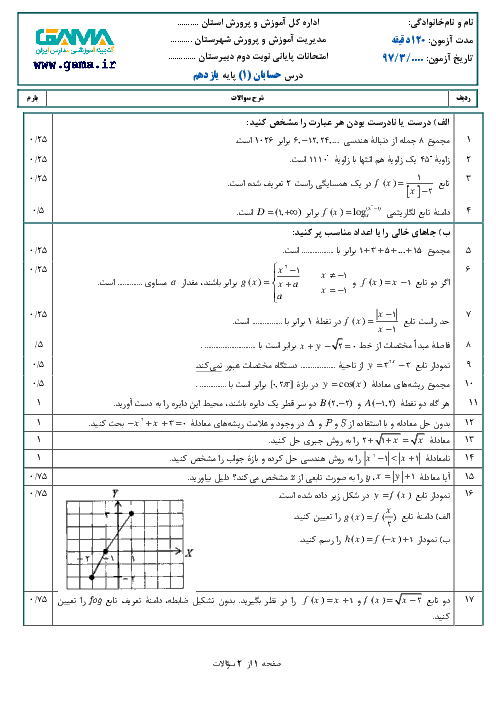
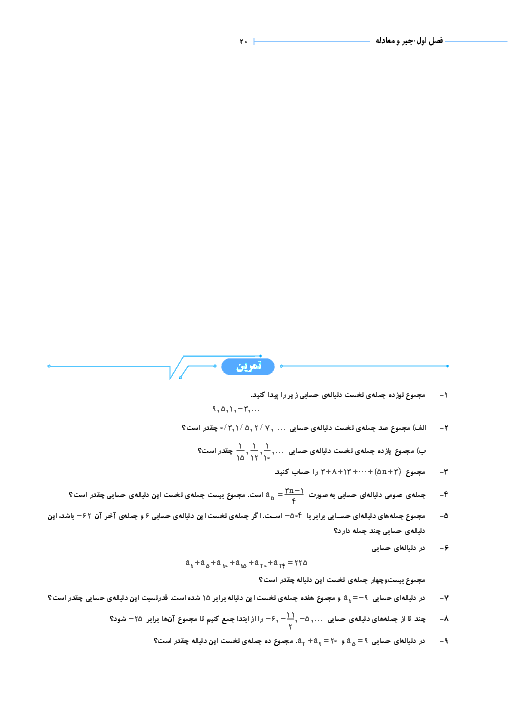
$\begin{align} & x\rangle -1\Rightarrow x+2\rangle 1\rangle 0\Rightarrow y=f(x)=1-(x+2)\Rightarrow y=-1y\le 0 \\ & y=-x-1\Rightarrow x=-1-y\Rightarrow {{f}^{-1}}(x)=-1-xx\le 0 \\ \end{align}$
$\text{ }\!\!\{\!\!\text{ }{{D}_{go{{f}^{-1}}}}=\left\{ x\in {{D}_{{{f}^{-1}}}}\left| {{f}^{-1}} \right. \right.(x)\in \left. {{D}_{g}} \right\}=\left\{ x\le 0\left| -1-x\ne -1 \right. \right\}=\left\{ x\le 0\left| x\ne 0 \right. \right\}=\left\{ x\langle 0 \right\}=(-\infty ,0)$
$go{{f}^{-1}}(x)=g(-1-x)=\frac{-1-x+2}{-1-x+1}=\frac{1-x}{-x}=\frac{x-1}{x}x\langle 0$