قسمت 2: حرکت هماهنگ ساده
فیزیک (3) ریاضی
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
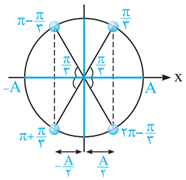
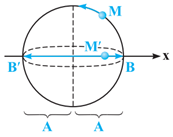
در شکل مقابل، متحرک $M$ بر روی یک دایره با بسامد زاویه‌ای ثابت می‌چرخد. در چه زاویه‌هایی با جهت مثبت محور $x$، تصویر این متحرک بر روی محور افقی $({M}')$ از مرکز نوسان، $\frac{A}{2}$ فاصله دارد؟ ($A$ برابر دامنهٔ نوسان است.)
1 )
$\frac{\pi }{6}$، $\frac{5\pi }{6}$، $\frac{7\pi }{6}$، $\frac{11\pi }{6}$، ...
$\frac{\pi }{3}$، $\frac{2\pi }{3}$، $\frac{4\pi }{3}$، $\frac{5\pi }{3}$، ...
3 )
$\frac{\pi }{4}$، $\frac{3\pi }{4}$، $\frac{5\pi }{4}$، $\frac{7\pi }{4}$، ...
4 )
$\frac{\pi }{2}$، $\frac{3\pi }{2}$، $\frac{5\pi }{2}$، $\frac{7\pi }{2}$، ...
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...