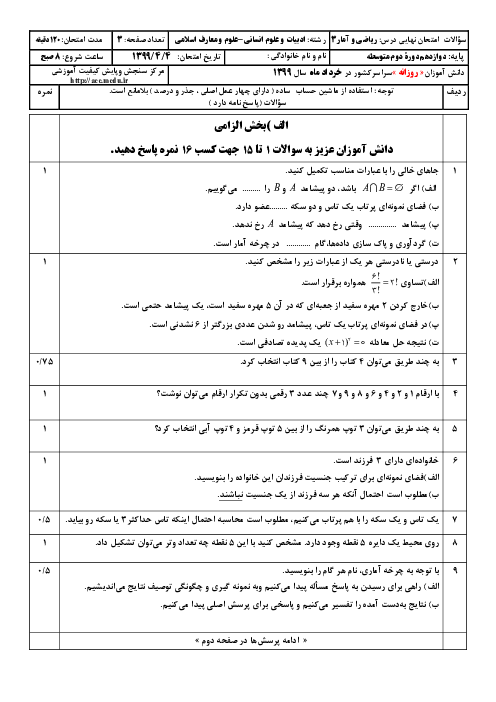
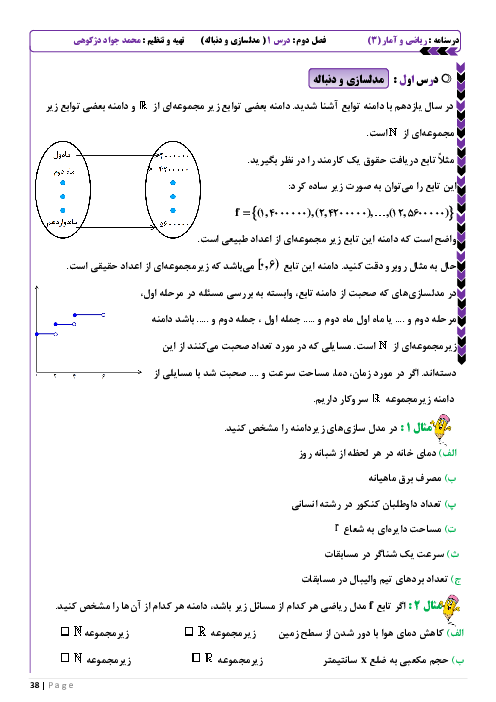
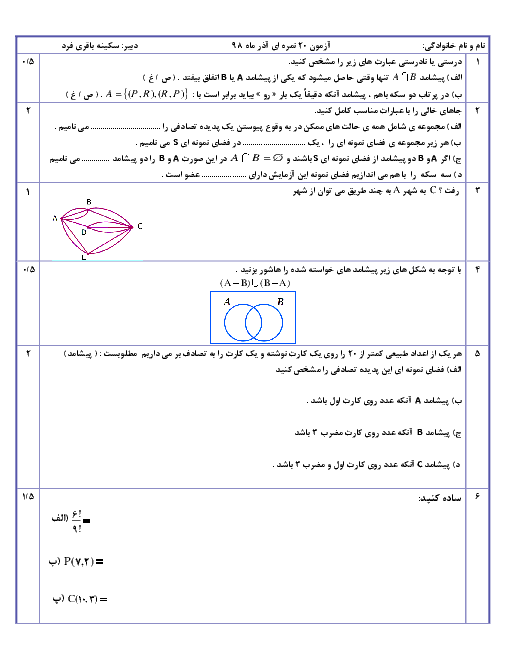
درس 2: دنبالههای حسابی
ریاضی و آمار (3)
دوازدهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
مجموع 5 جملۀ اول از یک دنبالۀ حسابی صعودی مساوی 60 و مجموع دو جملۀ بزرگتر سه برابر مجموع سه جملۀ کوچکتر است. قدر نسبت آن کدام است؟