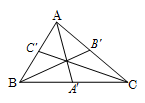
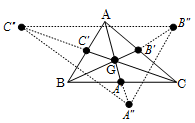
می‌دانيم ميانه‌ها يكديگر را به نسبت 2 به 1 قطع می‌كنند. اگر محل برخورد ميانه‌ها را $G$ بناميم، داريم: 

$\left\{ \begin{matrix} G{A}'=\frac{1}{3}A{A}'  \\ G{B}'=\frac{1}{3}B{B}'  \\ G{C}'=\frac{1}{3}C{C}'  \\ \end{matrix} \right.,\left\{ \begin{matrix} GA=\frac{2}{3}A{A}'  \\ GB=\frac{2}{3}B{B}'  \\ GC=\frac{2}{3}C{C}'  \\ \end{matrix} \right.$

از طرفی بنابر فرض مسأله ${B}'{B}''=\frac{2}{3}B{B}',{A}'{A}''=\frac{2}{3}A{A}'$ و ${C}'{C}''=\frac{2}{3}C{C}'$ است. بنابراین:

$\left\{ \begin{matrix} G{A}''=G{A}'+{A}'{A}''=\frac{1}{3}A{A}'+\frac{2}{3}A{A}'=A{A}'=\frac{3}{2}GA  \\ G{C}''=G{C}'+{C}'{C}''=\frac{1}{3}C{C}'+\frac{2}{3}C{C}'=C{C}'=\frac{3}{2}GC  \\ G{B}''=G{B}'+{B}'{B}''=\frac{1}{3}B{B}'+\frac{2}{3}B{B}'=B{B}'=\frac{3}{2}GB  \\ \end{matrix} \right.$

پس:

$\left| k \right|=\frac{G{A}''}{GA}=\frac{G{B}''}{GB}=\frac{G{C}''}{GC}=\frac{3}{2}$

$\xrightarrow[k\lt 0]{}k=-\frac{3}{2}$