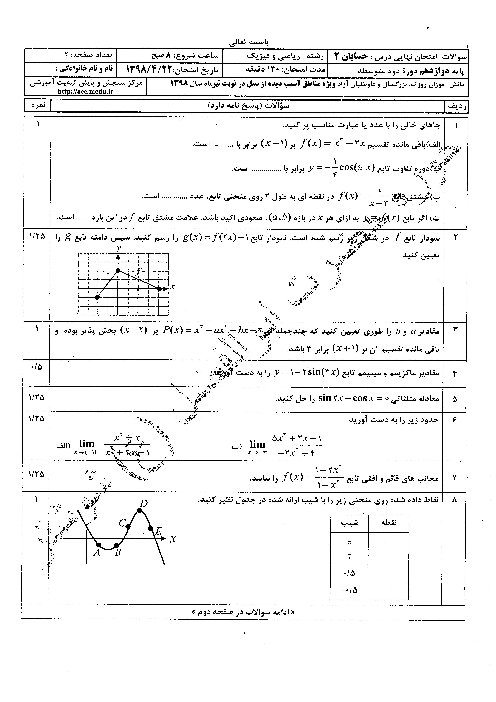
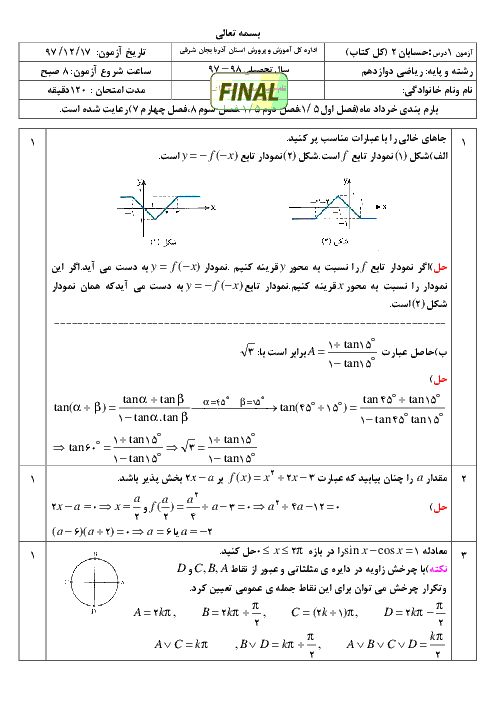
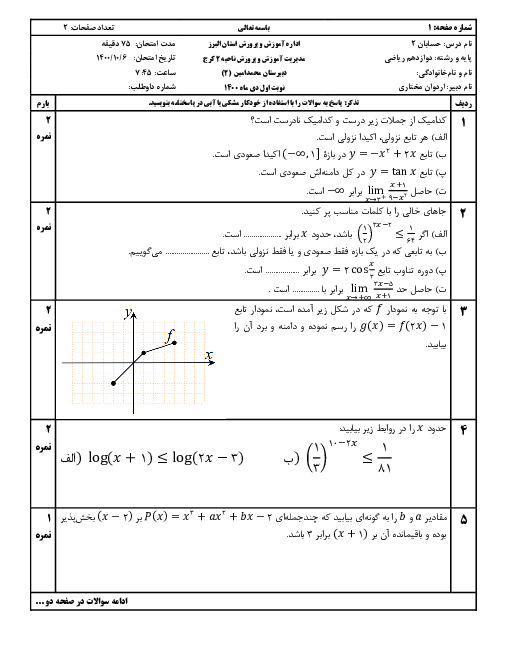
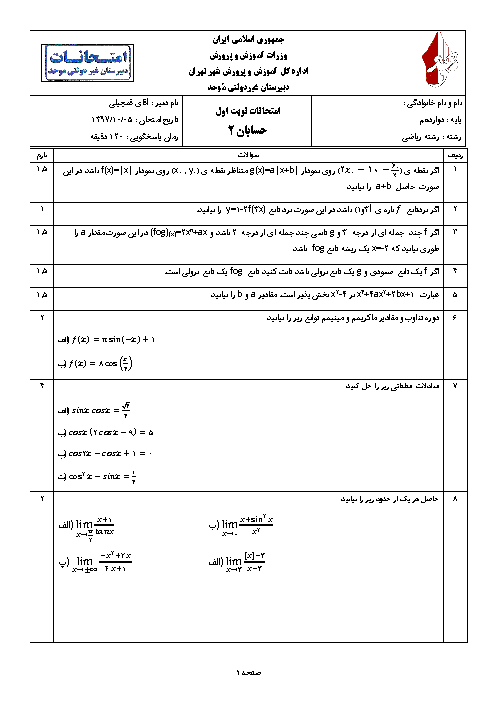
اگر $A(-1,2)$ مختصات اکسترمم نسبی تابع $f(x)=\frac{ax+b}{{{x}^{2}}+2x}$ باشد، کدام درست است؟
1 )
$A$ نقطهٔ مینیمم نسبی و $a+b=2$ است.
2 )
$A$ نقطهٔ ماکزیمم نسبی و $a+b=-2$ است.
$A$ نقطهٔ مینیمم نسبی و $a+b=-2$ است.
4 )
$A$ نقطهٔ ماکزیمم نسبی و $a+b=2$ است.
پاسخ تشریحی :
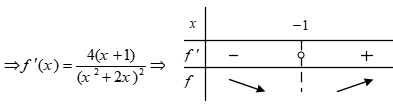
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!