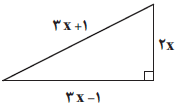درس 2: حل معادلۀ درجۀ 2 و کاربردها
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
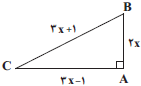
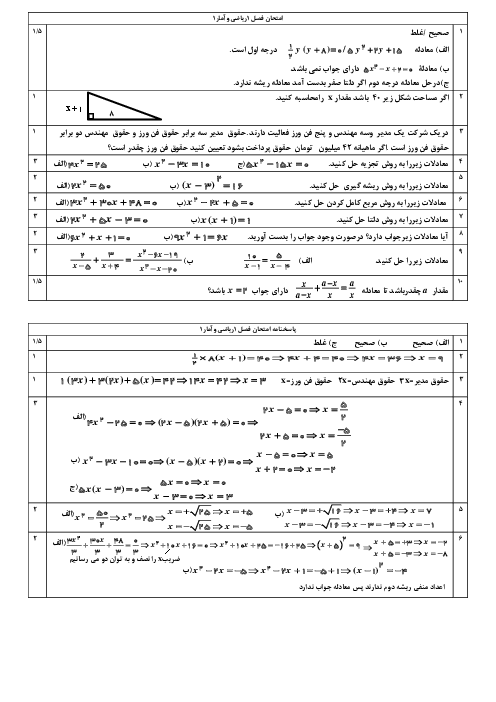
با توجه به طول اضلاع مثلث قائمالزاویه در شکل زیر، مساحت آن چند واحد مربع است؟