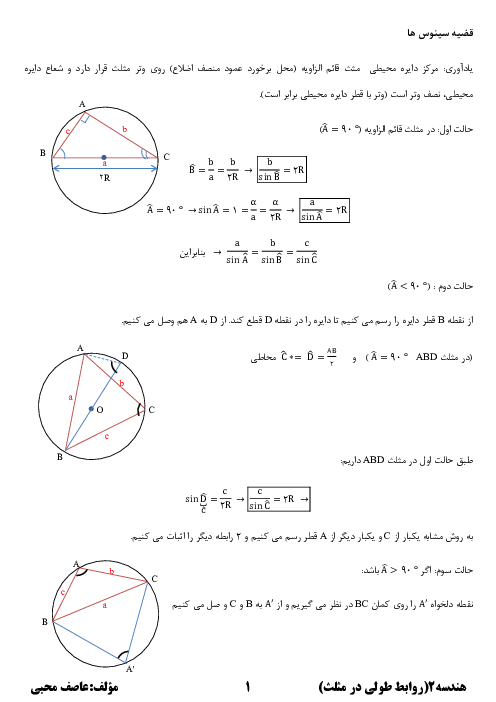
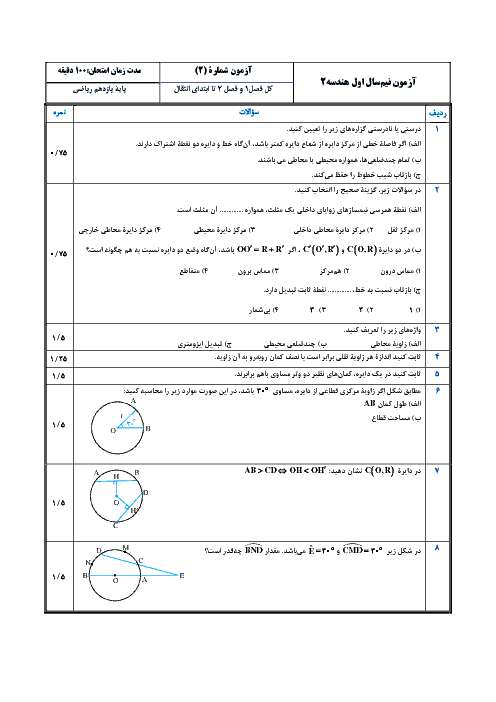
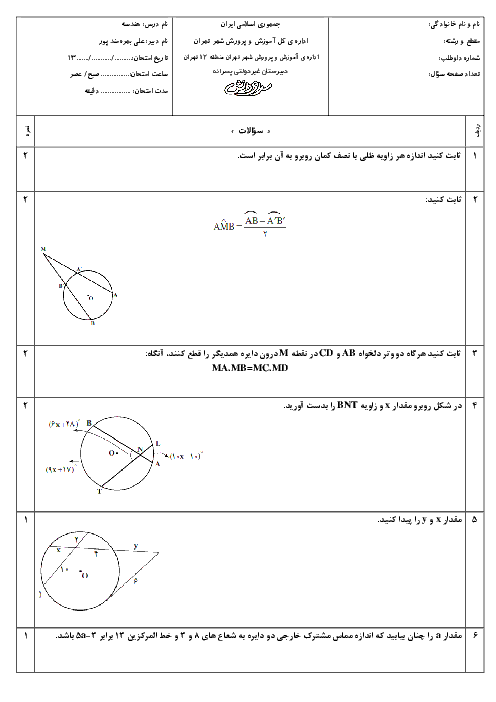
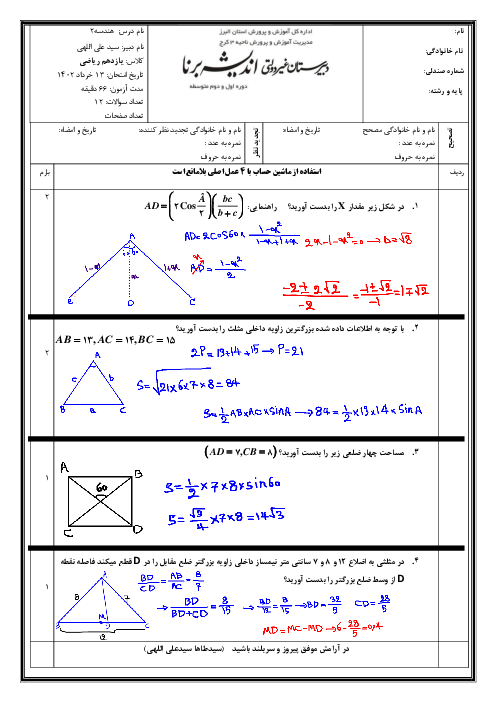
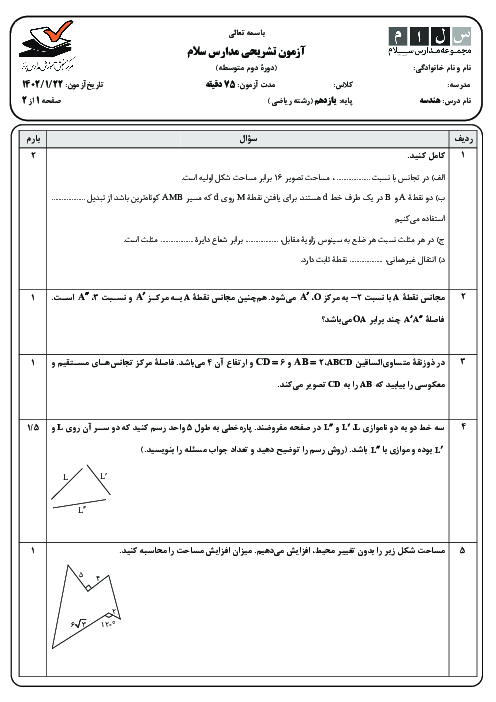
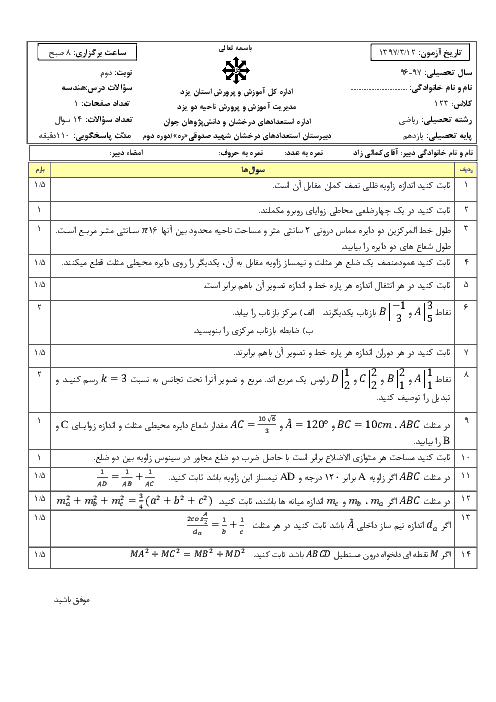
درس 4: قضیۀ هرون (محاسبۀ ارتفاعها و مساحت مثلث)
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
مساحت مثلث متساویالساقینی با زاویه رأس 30 درجه، 9 سانتیمتر مربع است. طول نیمساز و میانۀ وارد بر قاعدۀ این مثلث کدام است؟ ($\sin {{75}^{\circ }}=0/96$)