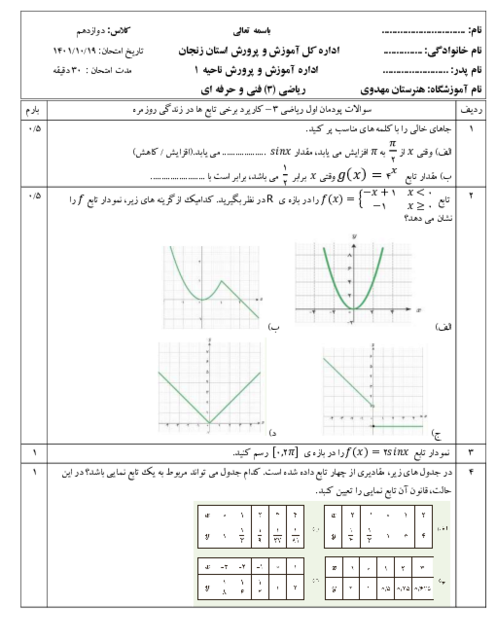
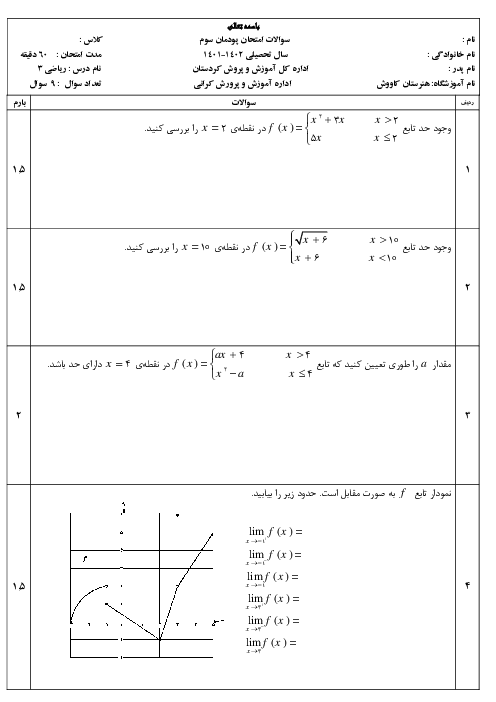
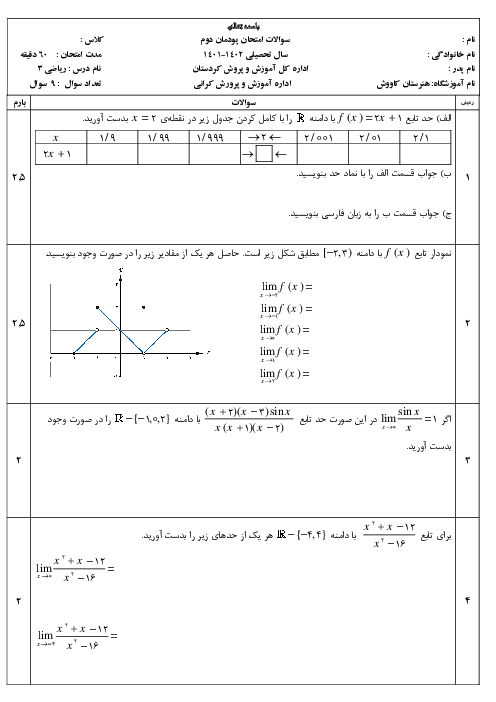
عبارت داده شده از سه بخش تشکیل شده که هر کدام را جداگانه به‌ دست می‌آوریم:

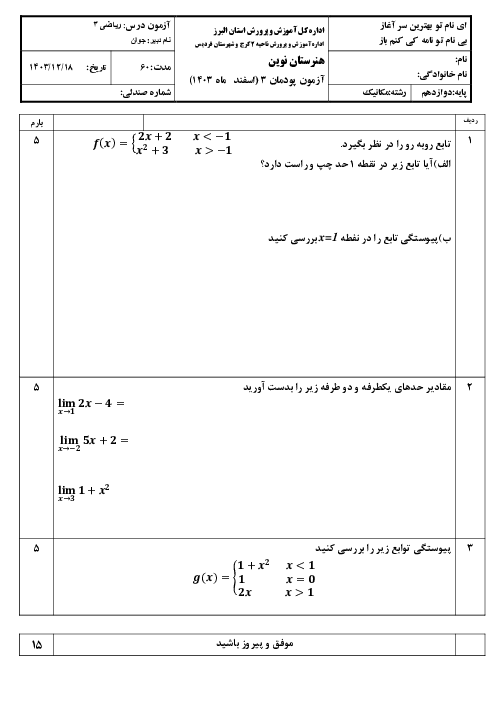
الف) محاسبه حد چپ یا همان بخش $\lim\limits_{x\to {{0}^{-}}}f\left( x \right)$:

در این قسمت شخص ناظر از سمت چپ محور xها به طرف نقطه صفر حرکت می‌کند در این‌ صورت مقدار y برابر 1 می‌شود:

$\lim\limits_{x\to {{0}^{-}}}f\left( x \right)=1$

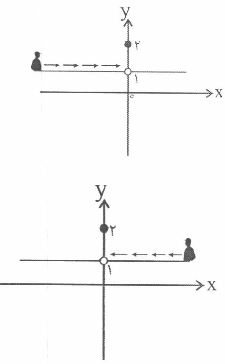
محاسبه حد راست یا همان بخش $\lim\limits_{x\to {{0}^{+}}}f\left( x \right)$:
شخص ناظر از سمت راست به طرف نقطه $x=0$ حرکت می‌کند مقدار y برابر 1 می‌شود:

$\lim\limits_{x\to {{0}^{+}}}f\left( x \right)=1$

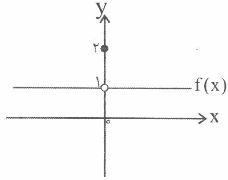
ج) محاسبه $f\left( 0 \right)$: منظور از $f\left( 0 \right)$ همان مقدار f در نقطه $x=0$ است که طبق شکل برابر 2 می‌شود $\left( f\left( 0 \right)=2 \right)$
نکته: در نقطه $x=0$ یک دایره تو خالی و یک دایره توپر روی محور yها قرار دارد که باید دایره توپر را در نظر گرفت یعنی نقطه 2 را.

د) حال مقادیر به‌ دست آمده را در صورت سؤال قرار می‌دهیم:

$\left. \begin{matrix}
   \lim\limits_{x\to {{0}^{-}}}f\left( x \right)=1  \\
   \lim\limits_{x\to {{0}^{+}}}f\left( x \right)=1  \\
   f\left( 0 \right)=2  \\
\end{matrix} \right\}\Rightarrow A=\lim\limits_{x\to {{0}^{-}}}f\left( x \right)+4f\left( 0 \right)+\lim\limits_{x\to {{0}^{+}}}f\left( x \right)=1+4\left( 2 \right)+1=10$