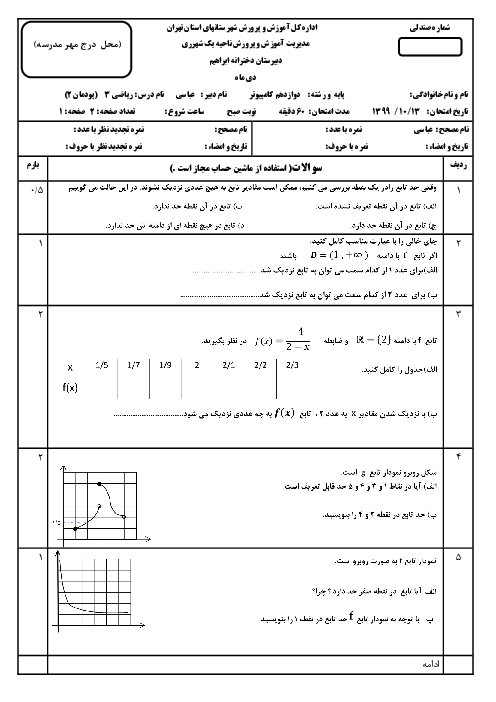
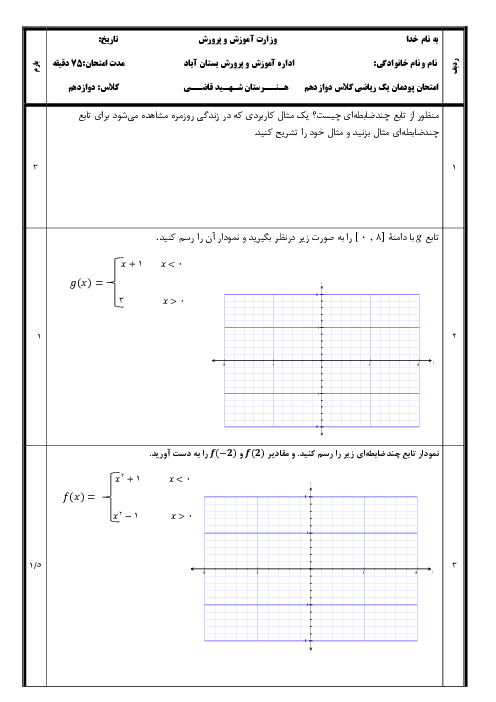
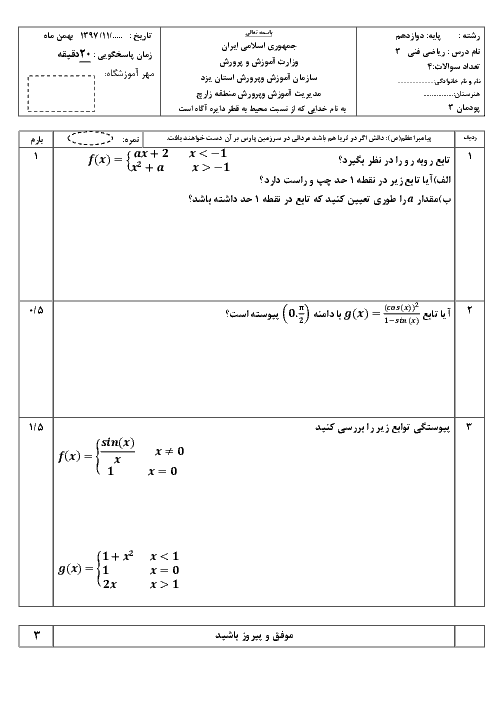
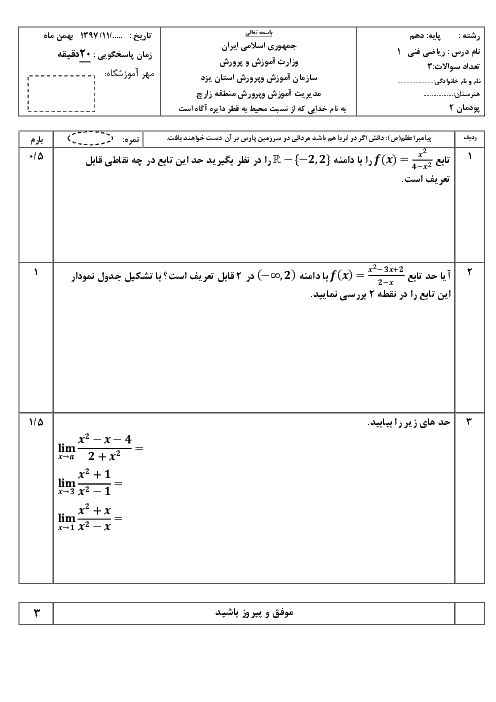
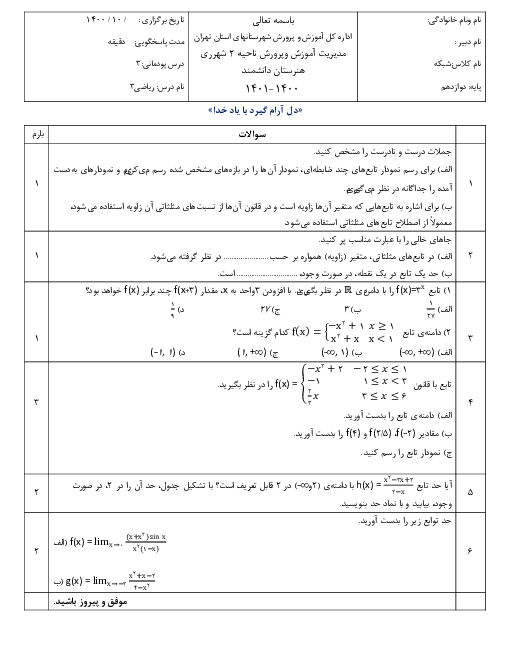
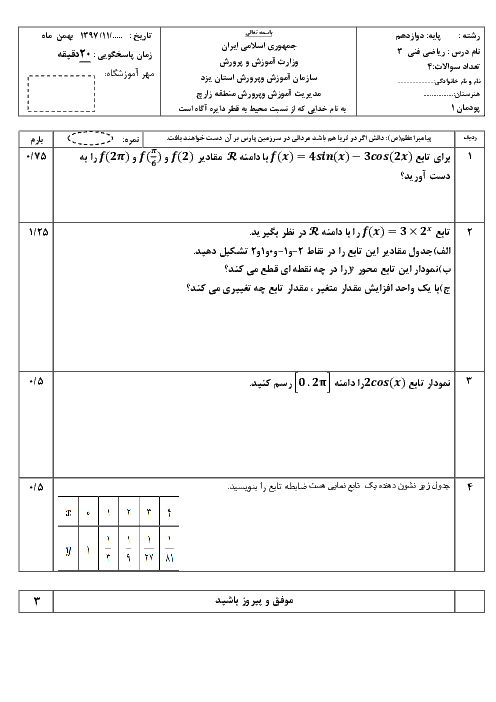
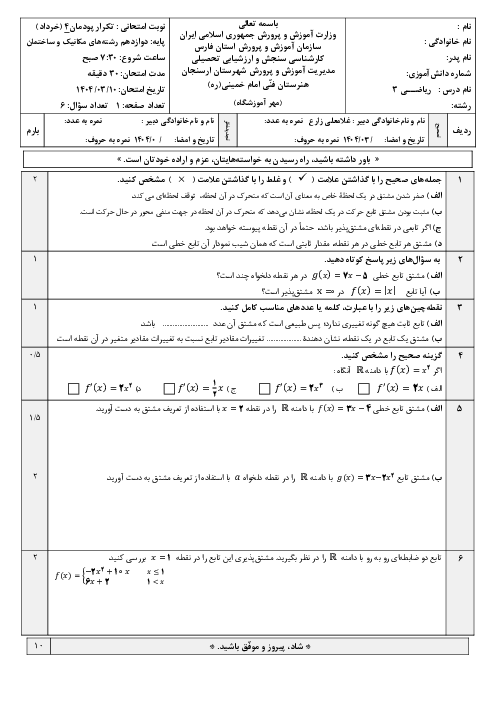
اگر تابع با ضابطهی $f\left( x \right)=\left\{ \begin{matrix} \frac{{{x}^{2}}-1}{\left| x-1 \right|}\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,x\ne 1 \\ a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,\,x=1 \\\end{matrix} \right.$ باشد به ازای کدام مقدار a در $x=1$ پیوسته است؟