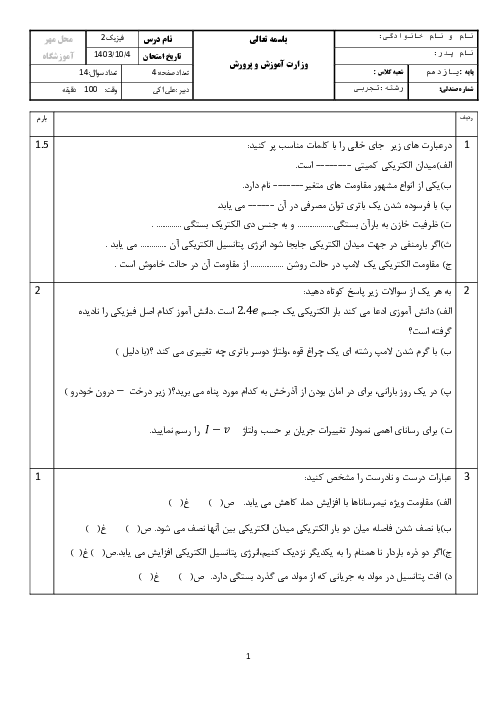
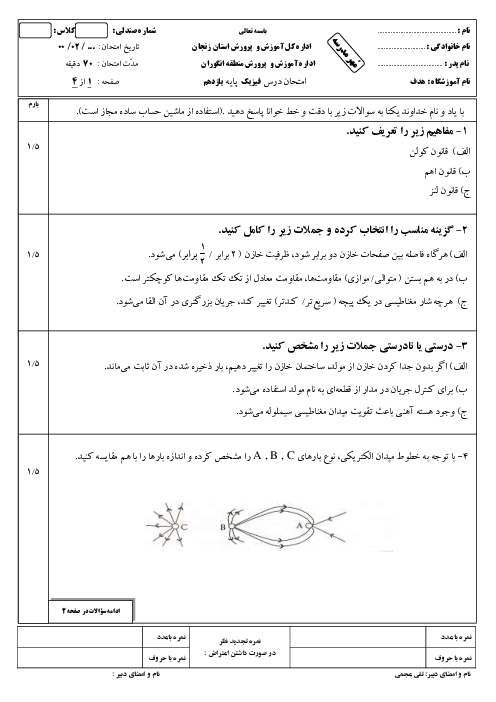
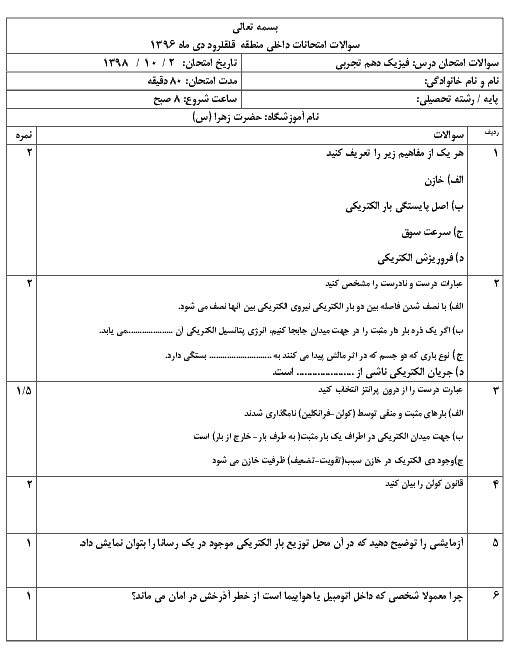
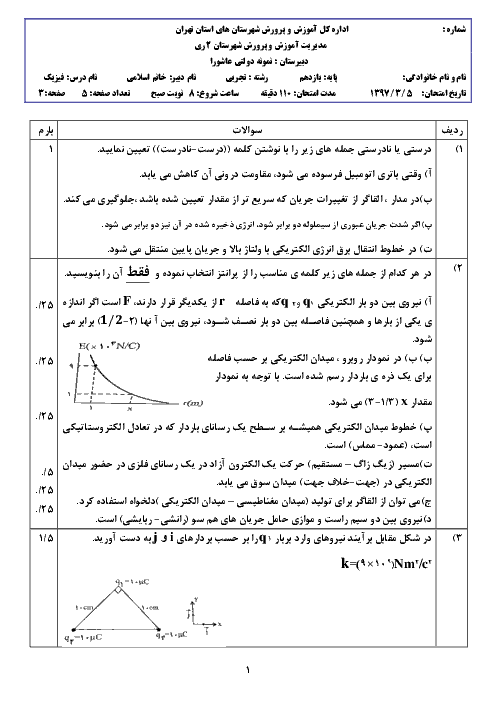
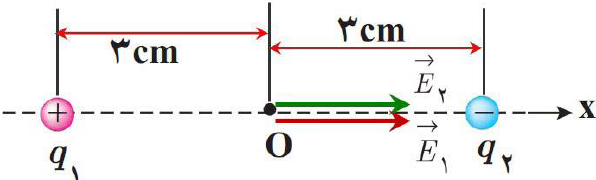
دو بار الکتریکی نقطهای غیر همنام ${{q}_{1}}=+1/0nc$ و ${{q}_{2}}=-1/0nc$ مطابق شکل زیر به فاصلهی 6/0cm از یکدیگر قرار دارند. اندازه میدان الکتریکی برآیند را در نقطه o دست آورید.
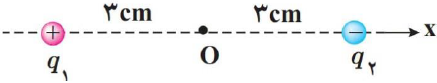
پاسخ تشریحی :
ابتدا جهت میدانهای الکتریکی ${{\overrightarrow{E}}_{1}},{{\overrightarrow{E}}_{2}}$ را در نقطهی O تعیین میکنیم. برای این کار در نقطه O یک بار الکتریکی مثبت فرض میکنیم و نیروی وارد بر این بارِ فرضی را که از طرف سایر بارها ایجاد میشود، مشخص میکنیم. جهت میدان الکتریکی نیز در جهت این نیروها است.
حال به کمک رابطهی اندازهی تکتک این میدانهای الکتریکی را به دست میآوریم و سپس به کمک روابط جمع برداری، بردار میدان الکتریکی برآیند و اندازهی بردار میدان الکتریکی برآیند را به دست میآوریم.
${{E}_{1}}=k\frac{\left| {{q}_{1}} \right|}{r_{1}^{2}}\to {{E}_{1}}=9\times {{10}^{9}}\times \frac{1\times {{10}^{-9}}}{{{\left( 3\times {{10}^{-2}} \right)}^{2}}}\to {{E}_{1}}=1\times {{10}^{4}}\frac{N}{C}\to {{\overrightarrow{E}}_{1}}=(1\times {{10}^{4}})\overrightarrow{i}+0\overrightarrow{j}$
${{E}_{2}}=k\frac{\left| {{q}_{2}} \right|}{r_{2}^{2}}\to {{E}_{2}}=9\times {{10}^{9}}\times \frac{1\times {{10}^{-9}}}{{{\left( 3\times {{10}^{-2}} \right)}^{2}}}\to {{E}_{2}}=1\times {{10}^{4}}\frac{N}{C}\to {{\overrightarrow{E}}_{2}}=(1\times {{10}^{4}})\overrightarrow{i}+0\overrightarrow{j}$
${{\overrightarrow{E}}_{0}}={{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=\left( (1\times {{10}^{4}})\overrightarrow{i}+\overrightarrow{0j} \right)+\left( (1\times {{10}^{4}})\overrightarrow{i}+\overrightarrow{0j} \right)=\left( (2\times {{10}^{4}})\overrightarrow{i}+\overrightarrow{0j} \right)$
$\overrightarrow{{{E}_{0}}}=\sqrt{{{E}_{ox}}^{2}{{E}_{oy}}^{2}}=2\times {{10}^{4}}\frac{N}{C}$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!