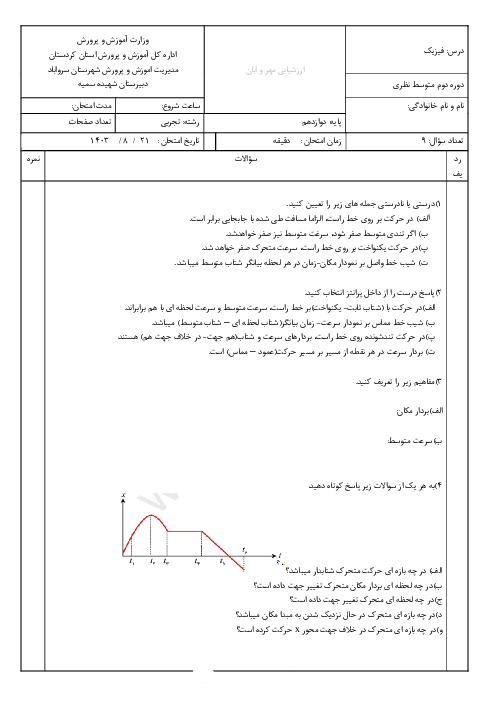
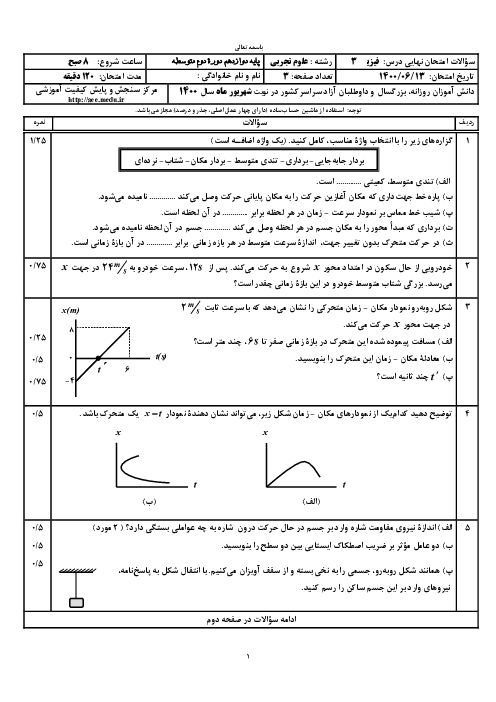
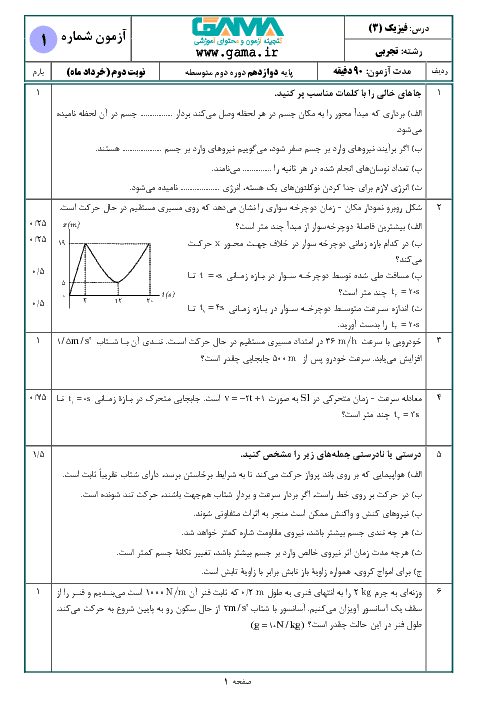
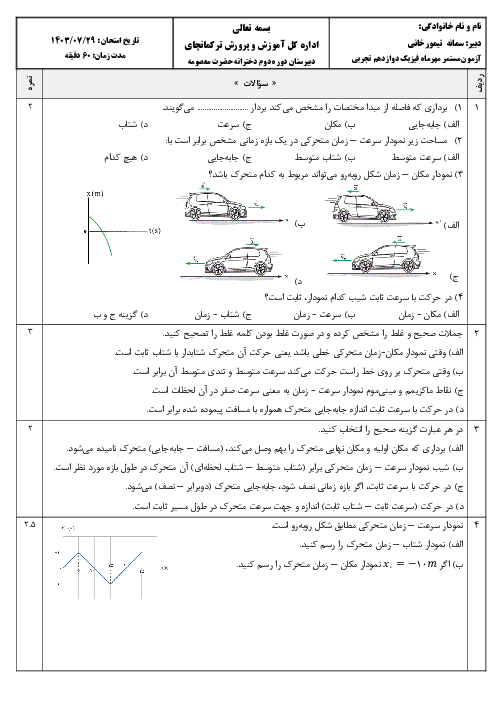
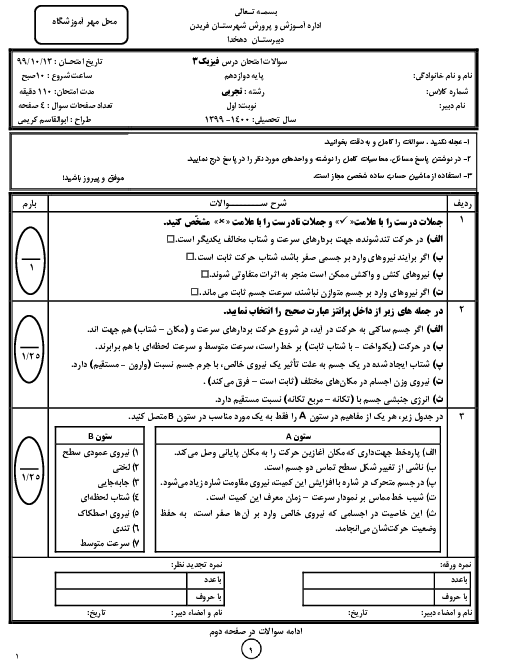
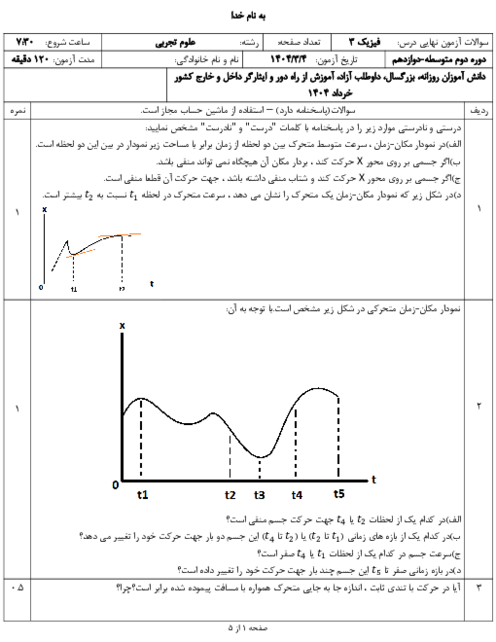
با توجه به آنکه صوت چشمه در تمام جهت‌ها یکنواخت پخش می‌شود، جبهه‌ی موج صوتی کروی خواهد بود و در رابطه‌ی $I=\frac{\overrightarrow{P}}{A}$، $A$ سطح کره‌ای است که شعاع آن $(d)$ برابر با فاصله‌ی شنونده تا چشمه است.

$\begin{matrix}    I=\frac{\overline{P}}{A}=\frac{\overline{P}}{4\pi {{d}^{2}}}\Rightarrow  frac{{{I}_{2}}}{{{I}_{1}}}=\frac{\frac{\overline{P}}{4\pi d_{2}^{2}}}{\frac{\overline{P}}{4\pi d_{1}^{2}}}={{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}  \\    \left. \begin{matrix}    {{\beta }_{1}}=10\log \frac{{{I}_{1}}}{{{I}_{{}^\circ }}}  \\    {{\beta }_{2}}=10\log \frac{{{I}_{2}}}{{{I}_{{}^\circ }}}  \\ \end{matrix} \right\}\Rightarrow {{\beta }_{2}}-{{\beta }_{1}}=10\log \frac{\frac{{{I}_{2}}}{{{I}_{{}^\circ  }}}{\frac{{{I}_{1}}}{{{I}_{{}^\circ }}}}=10\log \frac{{{I}_{2}}}{{{I}_{1}}}=10\log  {(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}\Rightarrow 12=10\log {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}\Rightarrow 1/2=\log {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}  \\ \end{matrix}$ 

$4\times 0/3=\log {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}\Rightarrow 4\times \log 2=\log {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}\Rightarrow \log {{2}^{4}}=\log {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}\Rightarrow {{(\frac{{{d}_{1}}}{{{d}_{2}}})}^{2}}={{2}^{4}}$

$\Rightarrow \frac{{{d}_{1}}}{{{d}_{2}}}={{2}^{2}}\Rightarrow \frac{400}{{{d}_{2}}}=4\Rightarrow {{d}_{2}}=100m\Rightarrow {{d}_{2}}-{{d}_{1}}=100-400=-300m$