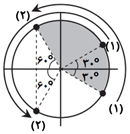
$x=A\operatorname{Cos}\omega t\Rightarrow \frac{x}{A}=\operatorname{Cos}\omega t\Rightarrow \left\{ \begin{matrix} {{x}_{1}}=+\frac{\sqrt{3}}{2}A\Rightarrow \operatorname{Cos}\omega t=+\frac{\sqrt{3}} {2}\Rightarrow \omega {{t}_{1}}={{\theta }_{1}}=\pm \frac{\pi }{6}rad  \\ {{x}_{2}}=-\frac{A}{2}\Rightarrow \operatorname{Cos}\omega t=-\frac{1}{2}\Rightarrow \omega {{t}_{2}}={{\theta }_{2}}=\pm \frac{2\pi }{3}rad  \\ \end{matrix} \right.$

حداقل کمانِ مربوط به حالتی که نوسانگر پس از یک بار تغییر جهت، عبارت است از:

$\Delta \theta =\frac{2\pi }{3}-(-\frac{\pi }{6})=\frac{5\pi }{6}rad$

$\Delta \theta =\frac{2\pi }{T}\Delta t\Rightarrow \frac{5\pi }{6}=\frac{2\pi }{T}\Delta t\Rightarrow \Delta t=\frac{5T}{12}$