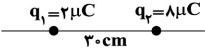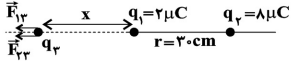با توجه به اینکه اندازۀ نیروی خالص 2 برابر نیروی $$${{F}_{13}}$ است، می‌توان نتیجه گرفت که نیروهایی که ${{q}_{1}}$ و ${{q}_{2}}$ به ${{q}_{3}}$ وارد می‌کنند، هم‌اندازه و هم‌جهت هستند. برای اینکه به بار ${{q}_{3}}$ دو نیروی هم‌اندازه و هم‌جهت وارد شود، باید ${{q}_{3}}$ خارج از فاصلۀ دو بار و نزدیک به بار کوچکتر باشد. با فرض اینکه ${{q}_{3}}$ مثبت است، نیروها همانند شکل خواهد بود. البته اگر ${{q}_{3}}$ منفی باشد، فقط جهت نیروها عکس می‌شود.

$$$\vec{F}=2{{\vec{F}}_{13}}={{\vec{F}}_{13}}+{{\vec{F}}_{23}}\Rightarrow {{\vec{F}}_{13}}={{\vec{F}}_{23}}$

اگر فاصله از بار ${{q}_{1}}$ را x بنامیم در این حالت خواهیم داشت:

${{\vec{F}}_{13}}={{\vec{F}}_{23}}\Rightarrow \frac{\cancel{k}\left| {{q}_{1}} \right|\cancel{\left| {{q}_{3}} \right|}}{{{x}^{2}}}=\frac{\cancel{k}\left| {{q}_{2}} \right|\cancel{\left| {{q}_{3}} \right|}}{(r+x)}\Rightarrow \frac{{{\cancel{2}}^{1}}}{{{x}^{2}}}=\frac{{{\cancel{8}}^{4}}}{{{(r+x)}^{2}}}$

از طرفین رابطه جذر می‌گیریم:

$\frac{1}{x}=\frac{2}{r+x}\Rightarrow 2x=r+x\Rightarrow x=r$

یعنی فاصلۀ نقطۀ موردنظر از بار ${{q}_{1}}$ برابر 30cm و از بار ${{q}_{2}}$ ، 60cm خواهد بود.