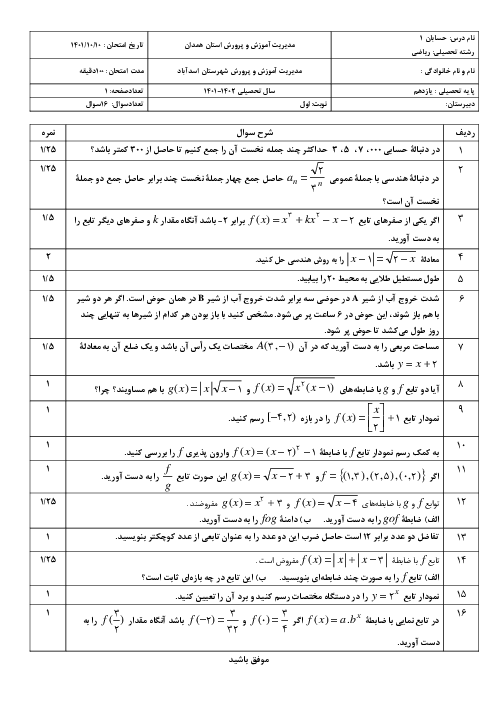
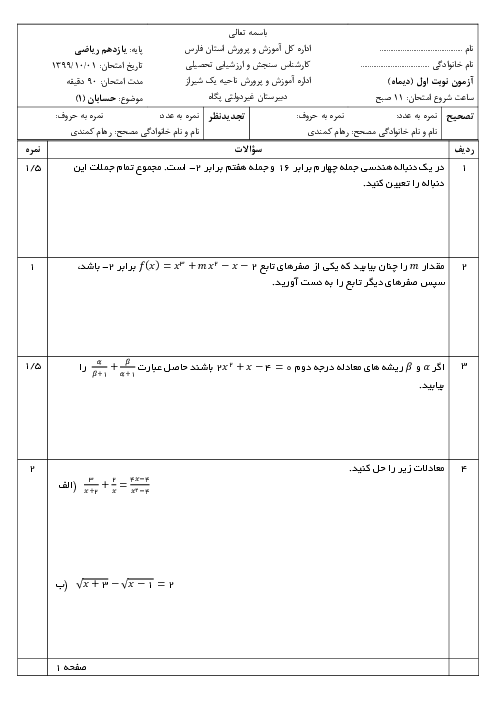
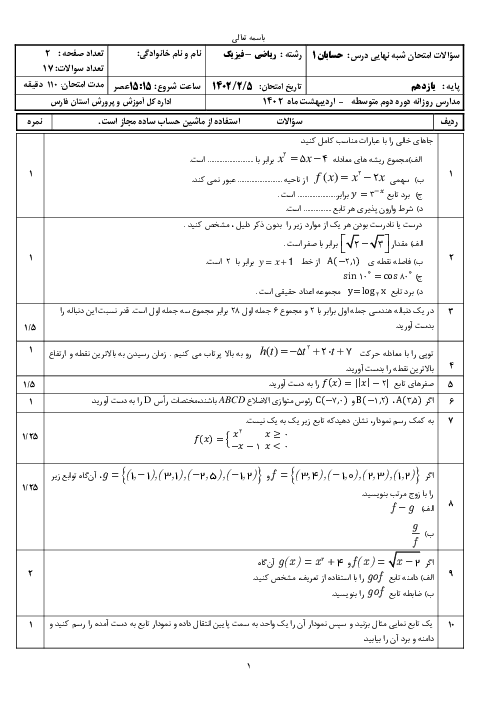
درس 1: مجموع جملات دنبالههای حسابی و هندسی
حسابان (1)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
حاصل ضرب چند جملۀ اول دنبالۀ هندسی $\sqrt{2},2,2\sqrt{2},...$ برابر با $4^{69}$ است؟