نمودار تابع به صورت زیر است. کدام است؟ | ریاضی (2) یازدهم شماره 47394 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم سوالات امتحان نهایی هماهنگ نهم نمونه سوال گام به گام کاربرگ نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 1: آشنایی با برخی از انواع توابع ریاضی (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

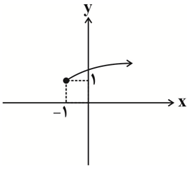
نمودار تابع $f(x)=a+\sqrt{x+b}$ به صورت زیر است. $f(\frac{5}{4})$ کدام است؟

1 )

2

2 )

$\frac{5}{2}$

3 )

3

4 )

$\frac{7}{2}$

نمایش پاسخ

با توجه به نمودار، دامنهٔ تابع $x\ge -1$ است. با توجه به ضابطهٔ تابع، دامنهٔ تابع برابر است با:

$x+b\ge 0\Rightarrow x\ge -b\xrightarrow{x\ge -1}b=1$

از طرفی با توجه به نمودار $f(-1)=1$، پس:

$f(x)=a\sqrt{x+b}\Rightarrow f(-1)=a+\sqrt{-1+b}=1$

$\xrightarrow{b=1}a=1\Rightarrow f(x)=1+\sqrt{x+1}$

$\Rightarrow f\left( \frac{5}{4} \right)=1+\sqrt{\frac{5}{4}+1}=1+\sqrt{\frac{9}{4}}=1+\frac{3}{2}=\frac{5}{2}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1401/04/16

یوسف شاکر اردکانی

ویدیو دوره آموزشی، ریاضی (2) یازدهم دوره دوم متوسطه- نظری

مدرس: محمد ابراهیمی علویجه

مدت دوره: 26 ساعت (38 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

23 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال شبه نهایی ریاضی (2) یازدهم تجربی

ويژه نامه نوبت اول و…

سوپراستار

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی 1399

18 صفحه

9 سری آزمون نوبت اول ریاضی (2) یازدهم تجربی دبیرستان سادات موسوی | دی…

داوود شهریاری

جزوه فصل 2: هندسه | ریاضی یازدهم تجربی

9 صفحه

جزوه فصل 2: هندسه | ریاضی یازدهم تجربی

امیرمحمد فکور

نمونه سوال فصل اول ریاضی 2 یازدهم تجربی دبیرستان آقا مصطفی خمینی | هندسه تحلیلی و جبر

5 صفحه

نمونه سوال فصل اول ریاضی 2 یازدهم تجربی دبیرستان آقا مصطفی خمینی | هندسه…

محمد مددی

آزمون نوبت اول ریاضی 2 پایه یازدهم رشته علوم تجربی دیماه 1402 مدرسه اسماء

4 صفحه

آزمون نوبت اول ریاضی 2 پایه یازدهم رشته علوم تجربی دیماه 1402 مدرسه اسماء

سمیه قربانی

رایـــــگان

امتحان مستمر ریاضی (2) پایۀ یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین | فصل چهارم: مثلثات ( درس 1 و 2 )

2 صفحه

امتحان مستمر ریاضی (2) پایۀ یازدهم رشتۀ تجربی دبیرستان پاسداران قزوین…

حسن کلهر

امتحان داخلی ریاضی (2) یازدهم تجربی دبیرستان کوثر | فصل 6 (حد و پیوستگی)

6 صفحه

امتحان داخلی ریاضی (2) یازدهم تجربی دبیرستان کوثر | فصل 6 (حد و پیوستگی)

خدیجه اقدامی مقدم

تمرین های تکمیلی فصل 2 ریاضی (2) یازدهم تجربی | درس 3: تشابه مثلث‌ها

4 صفحه

تمرین های تکمیلی فصل 2 ریاضی (2) یازدهم تجربی | درس 3: تشابه مثلث‌ها

محمدرضا آل سوف

نمونه سوال امتحان مستمر ریاضی (2) پایۀ یازدهم رشته تجربی دبیرستان علامه طباطبایی فلارد | فصل دوم: هندسه

2 صفحه

نمونه سوال امتحان مستمر ریاضی (2) پایۀ یازدهم رشته تجربی دبیرستان علامه…

سیدسبحان حسینی چمنی

تمرین های درس 3 از فصل دوم: تشابه مثلث ها | ریاضی یازدهم دبیرستان دانش فر

8 صفحه

تمرین های درس 3 از فصل دوم: تشابه مثلث ها | ریاضی یازدهم دبیرستان دانش…

اعظم نجف لو

موارد بیشتر

موارد بیشتر

ارسال فایل

وارون تابع ثابت را توضیح دهید.

مشکل در فهم لگاریتم فصل 5 ریاضی یازدهم

محاسبه شیب خطوط موازی با محورها در ریاضی یازدهم

موارد بیشتر

ارسال پرسش

موارد بیشتر