در شکل زیر، سهمی با رأس A و کانون F و خط هادی d رسم شده است. از F به نقطه دلخواه M روی سهمی وصل کرده و امتداد داده‌ایم تا d را در نقطه N قطع کند و از نقطه MT, M را بر d عمود کرده‌ایم.
ثابت کنید: $\frac{{FN}}{{FA}} = \frac{{2NT}}{{TH}}$
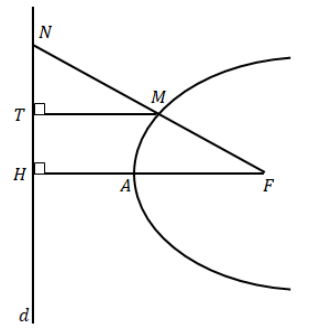
پاسخ تشریحی :
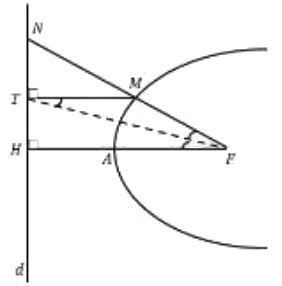
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...