درس 3: چند ضلعی‌های محاطی و محیطی
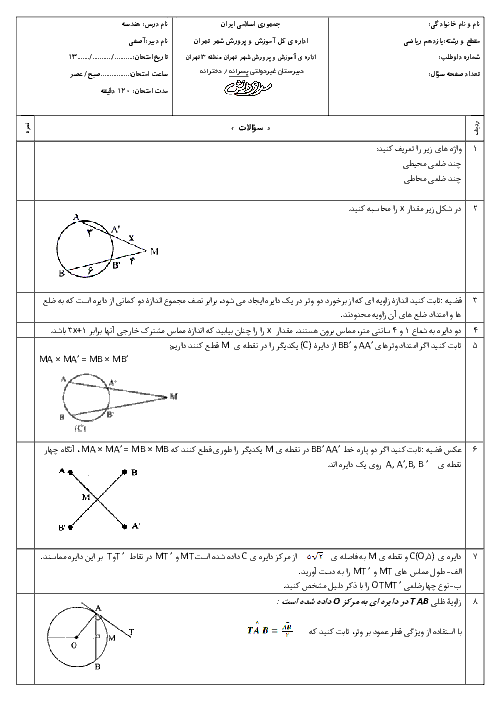
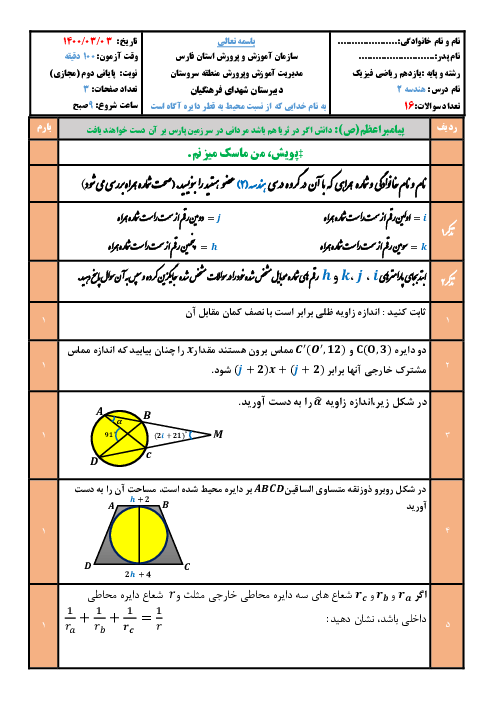
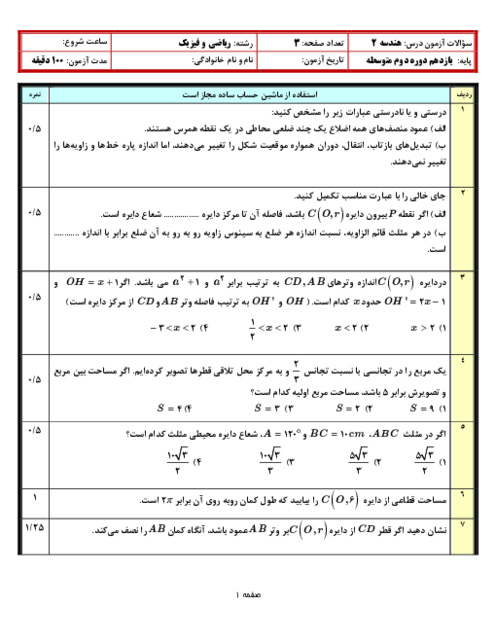
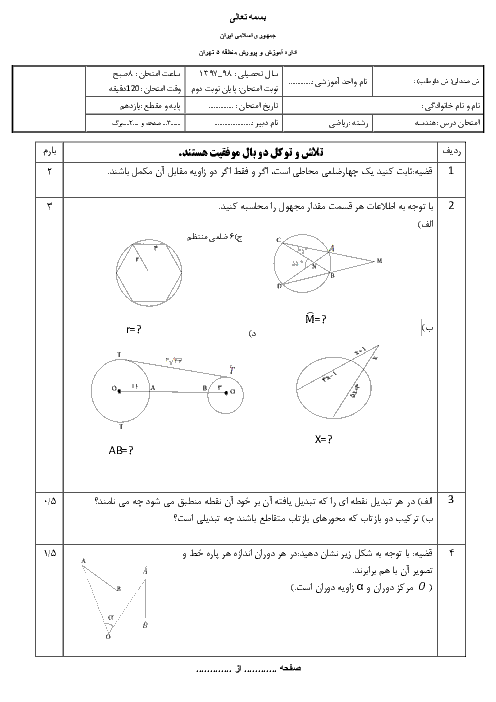
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
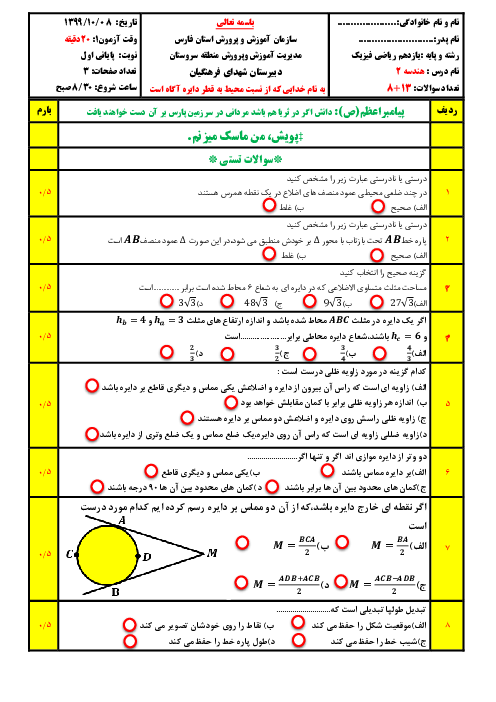
نسبت شعاع دايرهٔ محاطی يک شش ضلعی منتظم به شعاع دايرهٔ محيطی آن، كدام است؟
$\frac{\sqrt{3}}{2}$
2 )
$\frac{1}{2}$
3 )
$\cos {{15}^{\circ }}$
4 )
$\sin {{15}^{\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...