درس 2: وارون ماتریس و دترمینان
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
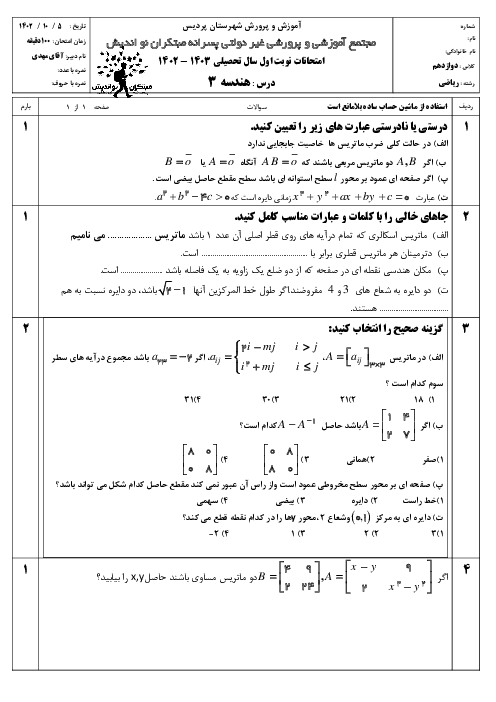
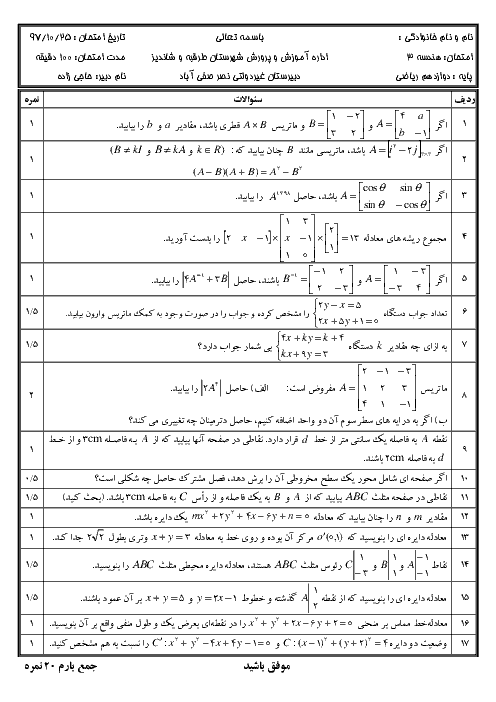
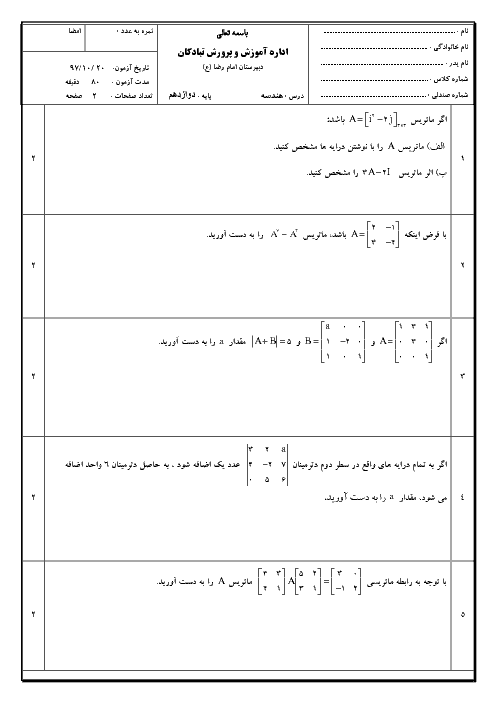
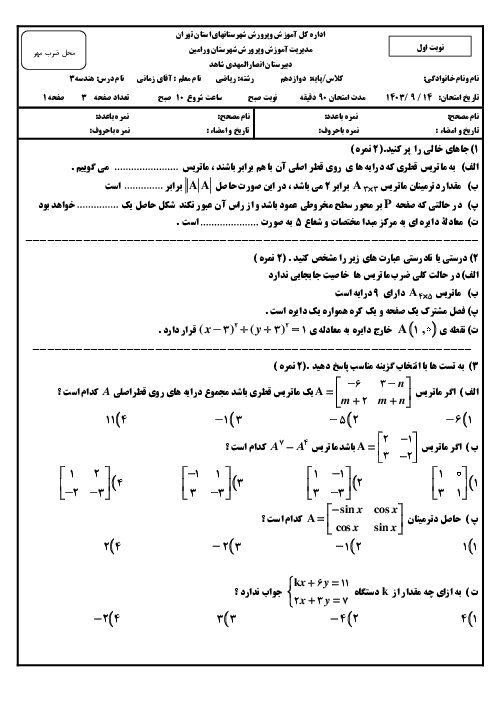
دو ماتریس $A = \left[ {\begin{matrix}
a & b & c \\
0 & d & 0 \\
e & 0 & f \\
\end{matrix} } \right]$ و $B = \left[ {\begin{matrix}
{ka} & {kb} & {kc} \\
0 & d & 0 \\
e & 0 & f \\
\end{matrix} } \right]$ (k عددی حقیقی است) را در نظر بگیرید. با محاسبه $|A|$ و $|B|$ نشان دهید که: $|B| = k|A|$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...