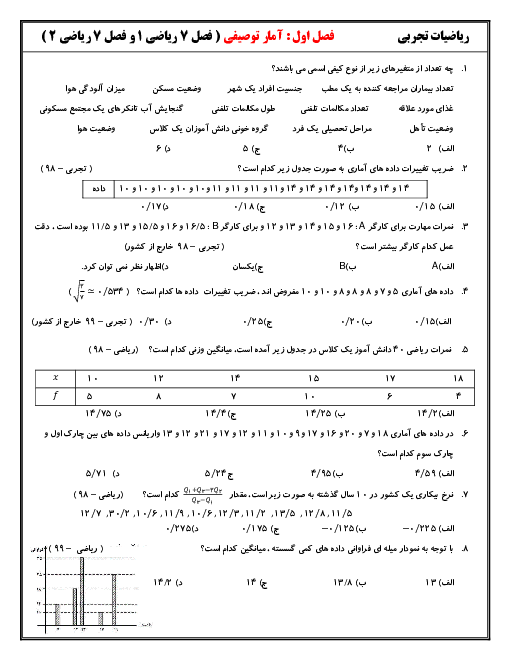
نمودار تابع $f(x) = {1 \over x}$ را در امتداد محور xها، 1 واحد در جهت مثبت و سپس قرینه آن نسبت به محور xها را در امتداد محور yها، 2 واحد در جهت منفی انتقال میدهیم. فاصله نقطههای برخورد منحنی حاصل با نمودار تابع f، از مبدأ مختصات، کدام است؟
1 )
${{\sqrt 2 } \over 2}$
2 )
${{\sqrt 5 } \over 2}$
3 )
${{3\sqrt 2 } \over 2}$
${{\sqrt {10} } \over 2}$