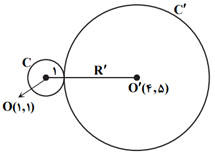
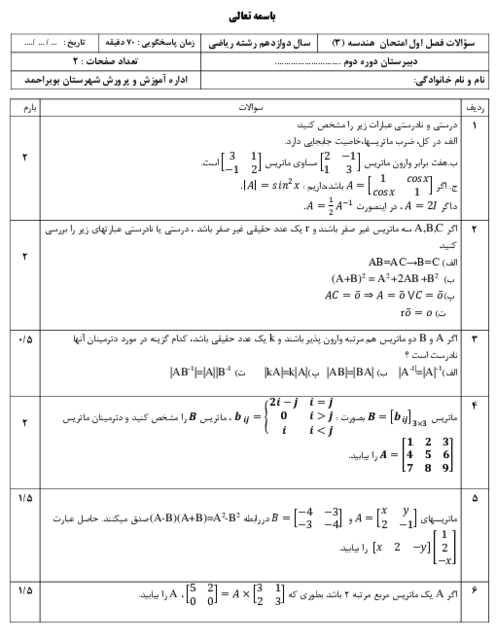
معادلۀ دايرهای كه نقطۀ $(4,5)$ مركز آن بوده و بر دايرهٔ ${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$ مماس خارج باشد، کدام است؟
1 )
${{x}^{2}}+{{y}^{2}}-8x-10y-32=0$
2 )
${{x}^{2}}+{{y}^{2}}-8x+10y-32=0$
${{x}^{2}}+{{y}^{2}}-8x-10y+25=0$
4 )
${{x}^{2}}+{{y}^{2}}-8x-10y-25=0$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...