$\operatorname{Sin}2x\operatorname{Sin}4x+{{\operatorname{Sin}}^{2}}x=1\Rightarrow \operatorname{Sin}2x(2\operatorname{Sin}2x\operatorname{Cos}2x)=1-{{\operatorname{Sin}}^{2}}x$

$\Rightarrow 2{{\operatorname{Sin}}^{2}}2x\operatorname{Cos}2x={{\operatorname{Cos}}^{2}}x\Rightarrow 2{{(2\operatorname{Sin}x\operatorname{Cos}x)}^{2}}\operatorname{Cos}2x={{\operatorname{Cos}}^{2}}x=0$

$\Rightarrow 8{{\operatorname{Sin}}^{2}}x{{\operatorname{Cos}}^{2}}x\operatorname{Cos}2x-{{\operatorname{Cos}}^{2}}x=0\Rightarrow {{\operatorname{Cos}}^{2}}x(8{{\operatorname{Sin}}^{2}}x\operatorname{Cos}2x-1)=0$

$\Rightarrow {{\operatorname{Cos}}^{2}}x=0*8{{\operatorname{Sin}}^{2}}x\operatorname{Cos}2x-1=0$

$8{{\operatorname{Sin}}^{2}}x\operatorname{Cos}2x-1=0\Rightarrow 8(\frac{1-\operatorname{Cos}2x}{2})\operatorname{Cos}2x-1=0\Rightarrow 4\operatorname{Cos}2x-4{{\operatorname{Cos}}^{2}}2x-1=0\Rightarrow \operatorname{Cos}2x=\frac{1}{2}$

$\Rightarrow 2x=2k\pi \pm \frac{\pi }{3}\Rightarrow x=k\pi \pm \frac{\pi }{6}$
$Cos^2x=0 \Rightarrow \operatorname{Cos}x=0\to x=k\pi +\frac{\pi }{2}$ 

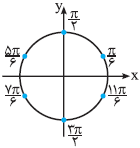
چون جواب‌های کلی داده شده، به ظاهر، شبیه جواب‌های کلی به‌دست آمده یعنی $x=k\pi +\frac{\pi }{2}$ و $x=k\pi \pm \frac{\pi }{6}$ نیست، پس باید بین این جواب‌ها اجتماع بگیریم. برای این منظور جواب‌های معادله را در یک دوره‌ی تناوب مثلاً در بازه‌ی $\left[ 0,2\pi  \right]$ به‌دست آورده و با جواب‌های خاص گزینه‌ها در بازه‌ی $\left[ 0,2\pi  \right]$ مقایسه می‌کنیم. اگر به‌جای $k$ در جواب‌های کلی $x=k\pi +\frac{\pi }{2}$ و $x=k\pi \pm \frac{\pi }{6}$، اعداد صحیح قرار دهیم، انتهای کمان مقابل به این زوایا به‌صورت نمایش داده شده در دایره‌ی زیر می‌باشند:

از بین این گزینه‌ها، فقط انتهای کمان مقابل به جواب کلی $x=(2k+1)\frac{\pi }{6}$ به‌ازای اعداد صحیح $k$ بر زوایای به‌دست آمده منطبق هستند.