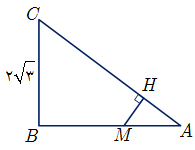
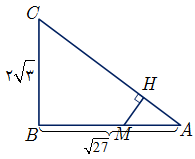
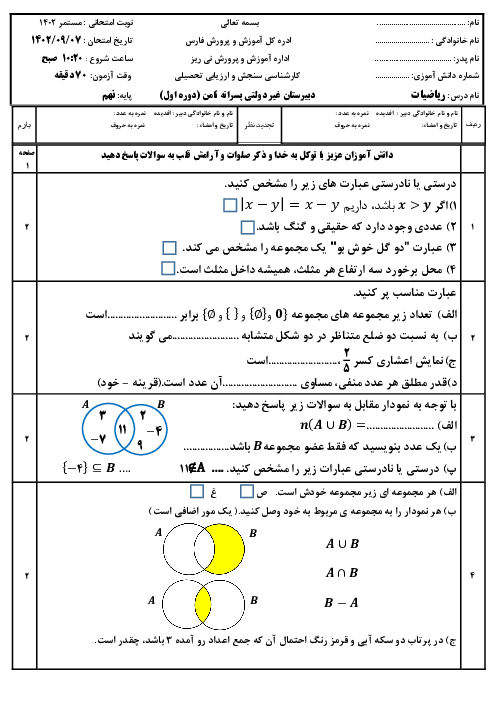
نسبت تشابه دو مثلث را با توجه به تساوی زاویه‌های آن‌ها و اضلاع روبه‌روی زاویه‌های برابر می‌نویسیم. بنابراین:

$\mathop {ABC}\limits^\Delta   = \mathop {AHM}\limits^\Delta   \Rightarrow \left\{ {\begin{array}{*{20}{c}}
  {\hat B = \hat H = {{90}^ \circ }} \\ 
  {\hat A = \hat A \Rightarrow \frac{{AC}}{{AM}} = \frac{{BC}}{{MH}} = \frac{{AB}}{{AH}}} \\ 
  {\hat M = \hat C} 
\end{array}} \right.$

با توجه به اطلاعات مسئله $AM = \frac{1}{3}AB = \frac{1}{3}\sqrt {27}  = \sqrt {\frac{{27}}{9}}  = \sqrt 3 $ و با توجه به رابطهٔ فیثاغورس داریم:

$\mathop {ABC}\limits^\Delta  :A{C^2} = A{B^2} + B{C^2} = {(\sqrt {27} )^2} + {(2\sqrt 3 )^2} = 27 + 12 = 39$

$ \Rightarrow AC = \sqrt {39}  \to \frac{{\sqrt {39} }}{{\sqrt 3 }} = \frac{{2\sqrt 3 }}{{MH}}$

$ \Rightarrow MH = \frac{6}{{\sqrt {39} }} \to \frac{6}{{\sqrt {39} }} \times \frac{{\sqrt {39} }}{{\sqrt {39} }} = \frac{{6\sqrt {39} }}{{39}} = \frac{{2\sqrt {39} }}{{13}}$